VELOCITY AND ACCELERATION IN AN ARBITRARILY MOVING FRAME

All of the reference frames with which we are concerned, except Fz of course, are in motion relative to inertial space. Fw and FB in particular have quite arbitrary motion, including acceleration of the origin, and rotation. Since in many applications, we want to express the position, inertial velocity,

and inertial acceleration of a particle in components parallel to the axes of these moving frames, we need general theorems that allow for arbitrary motion of the origin, and arbitrary angular velocity of the frame. These theorems are presented below.

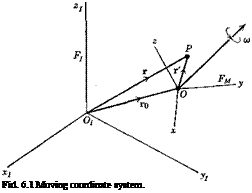
Let FM(Oxyz) be any moving frame with origin at 0 and with angular velocity ы relative to Fj. Let r = r0 + r’ be the position vector of a point P of FM (see Fig. 5.1). Then the velocity and acceleration of P relative to Fz are

(6.1Д)

We want expressions for the velocity and acceleration of P in terms of the components of r’ in FM. Expanding the first of (5.1,1)

vi = Kj + r’l, •/

— V Г 7

Of 1 *

where v0 = r 0 is the velocity of 0 relative to Fr The velocity components in

F M are given by

yM — ^МІУІ — ^mAXoi + rI> ~ VoM + ^М1*І

From the rule for transforming derivatives (4.6,10)

whence

vm = vom + *м + &мг’м (5.1,4)

The first term of (5.1,4) is the velocity of 0 relative to Fz, the second is the velocity of P relative to FM, and the last is the “transport velocity,”

i. e. the velocity relative to FT of the point of FM that is momentarily coincident with P. The total velocity of P relative to FT is the sum of these three components. Following traditional practice in flight dynamics, we denote

(When necessary, subscripts are added to the components to identify particular moving frames.)

The scalar expansion of (5.1,4) is then

Vx = v0x + X+ qz — ry

%, = vov + y + rx— Pz (5.1,6)

vz — voz + г + py — qx

These expressions then give the components, parallel to the moving coordinate axes, of the velocity of P relative to the inertial frame.

On differentiating v7 and using (5.1,4) we find the components of inertial acceleration parallel to the FM axes to be

&m = ^міуі = Vm + &мум

= V0M + v’m + + <ол/гм + й>муом ь*мг’м + &м&мгм

= aojf + rM + &mt’m + %G>m*m + &>м&мг’м (5.1,7)

where a„M — v0ji + й>муом — ^міуо, is the acceleration of 0 relative to Fr.

The total inertial acceleration of P is seen to be composed of the following parts:

a0: the acceleration of the origin of the moving frame r’: the acceleration of P relative to the moving frame tor’: the “tangential” acceleration owing to rotational acceleration of the frame FM

2tor’: the Coriolis acceleration to cor’: the centripetal acceleration

Three of the five terms vanish when the frame F M has no rotation, and only r’ remains if it is inertial. Note that the Coriolis acceleration is perpendicular to to and r’, and the centripetal acceleration is directed along the perpen­dicular from P to to. The scalar expansion of (5.1,7) gives the required inertial acceleration components of P as

ax = aox + * + 2 qz — 2 ry — x{q* + r2) + y(pq — r) + z(pr + q)

ау = аоу + У + 2rx — 2P* + X(P4 + *) — УІР2 + ri) + г(ЯГ — P) (5-1,8)

az = aoz + » + 2py — 2 qx + x(pr — q) + y(qr + P) — z(P2 + ?2)