Weathercock Stability (Yaw Stiffness)

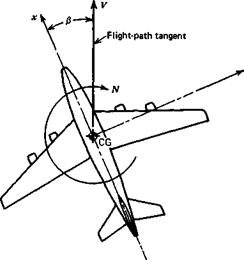
Application of the static stability principle to rotation about the г axis suggests that a stable airplane should have “weathercock” stability. That is, when the airplane is at an angle of sideslip /3 relative to its flight path (see Fig. 3.11), the yawing moment produced should be such as to tend to restore it to symmetric flight. The yawing mo­ment N is positive as shown. Hence the requirement for yaw stiffness is that ЭМЭ/3 must be positive. The nondimensional coefficient of N is

^ N Cn hpV2Sb

and hence for positive yaw stiffness dCJd/3 must be positive. The usual notation for this derivative is

This quantity is analogous in some respects to the longitudinal stability parameter Cnia. It is estimated in a similar way by synthesis of the contributions of the various components of the airplane. The principal contributions are those of the body and the vertical-tail surface. By contrast with Cma, the wing has little influence in most cases, and the CG location is a weak parameter. Whether or not a positive value of Cnfj will produce lateral stability can only be determined by a full dynamic analysis such as is done in Chap. 6.

78 Chapter 3. Static Stability and Control—Part 2

Some data for estimating the contribution of the body to C„ is contained in Ap­pendix B. There are also given data suitable for estimation of the lift-curve slope of the vertical-tail surface. This may be used to calculate the tail contribution as shown below.

In Fig. 3.12 are shown the relevant geometry and the lift force LF acting on the vertical tail surface. If the surface were alone in an airstream, the velocity vector F would be that of the free stream, so that (cf. Fig. 3.11) aF would be equal to — /3. When installed on an airplane, however, changes in both magnitude and direction of the local flow at the tail take place. These changes may be caused by the propeller slipstream, and by the wing and fuselage when the airplane is yawed. The angular de­flection is allowed for by introducing the sidewash angle a, analogous to the down – wash angle e. cr is positive when it corresponds to a flow in the у direction; that is, when it tends to increase aF. Thus the angle of attack is

aF = ~iв + a

and the lift coefficient of the vertical-tail surface is

CLf = aF(-p + cr) + arSr

The lift is then

(3.9,4)

and the yawing moment is

X

CG

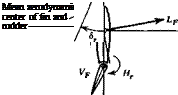У

(3.9,6)
CnF=-VvCLF[ —
and the corresponding contribution to the weathercock stability is
dCnF d/3	(т ЇЇ-ІІ
(3.9,7)