Circulation
The total amount of vortidty passing through any plane region within a flow field is called the circulation, Г. This is illustrated in Fig. 2.27 which shows a bundle of vortex tubes passing through a plane region of area A located in the flow field. The perimeter of the region is denoted by C. At a typical point P on the perimeter, the velocity vector is designated q or, equivalently, q. At P, the infinitesimal portion of C has length 6s and points in the tangential direction defined by the unit vector t (or F). It is important to understand that the region of area A and its perimeter C have no physical existence. Like the control volumes used for the application of conservation of mass and momentum, they are purely theoretical constructs.
Mathematically, the total strength of the vortex tubes can be expressed as an integral over the area A; thus
![]() Г = її n ■ SldA
Г = її n ■ SldA
A
where n is the unit normal to the area A. In two-dimensional flow the vortidty is in the z direction perpendicular to the two-dimensional flow field in the (x, y) plane. Thus n = к (i. e. the unit vector in the z direction) and ft = £k, so that Eqn (2.80) simplifies to
* Vortidty can also be created by other agencies, such as the presence of spatially varying body forces in the flow field. This could correspond to the presence of particles in the flow field, for example.
![]()
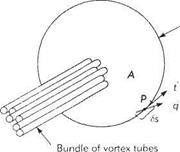
Fig. 2.27
Circulation can be regarded as a measure of the combined strength of the total number of vortex lines passing through A. It is a measure of the vorticity flux carried through A by these vortex lines. The relationship between circulation and vorticity is broadly similar to that between momentum and velocity or that between internal energy and temperature. Thus circulation is the property of the region A bounded by control surface C, whereas vorticity is a flow variable, like velocity, defined at a point. Strictly it makes no more sense to speak of conservation, generation, or transport of vorticity than its does to speak of conservation, generation, or transport of velocity. Logically these terms should be applied to circulation just as they are to momentum rather than velocity. But human affairs frequently defy logic and aerodynamics is no exception. We have become used to speaking in terms of conservation etc. of vorticity. It would be considered pedantic to insist on circulation in this context, even though this would be strictly correct. Our only motivation for making such fine distinctions here is to elucidate the meaning and significance of circulation. Henceforth we will adhere to the common usage of the terms vorticity and circulation.
In two-dimensional flow, in the absence of the effects of viscosity, circulation is conserved. This can be expressed mathematically as follows:
![]() £)( d( c>C_n
£)( d( c>C_n
or ox Oy
In view of what was written in Section 2.7.6 about the link between vorticity and viscous effects, it may seem somewhat illogical to neglect such effects in Eqn (2.82). Nevertheless, it is often a useful approximation to use Eqn (2.82).
Circulation can also be evaluated by means of an integration around the perimeter C. This can be shown elegantly by applying Stokes theorem to Eqn (2.81); thus
Г = Jjn-QdA = Jjn V x 4dA = ! q-tds (2.83)
This commonly serves as the definition of circulation in most aerodynamics text.
The concept of circulation is central to the theory of lift. This will become clear in Chapters 5 and 6.
Fig. 2.28
Example 2.2 For the rectangular region of a two-dimensional flow field depicted in Fig. 2.28, starting with the definition Eqn (2.81) of circulation, show that it can also be evaluated by means of the integral around the closed circuit appearing as the last term in Eqn (2.83).
From Eqns (2.76) and (2.81) it follows that











