Computation Models

The relations for the determination of the transport properties viscosity p and thermal conductivity k, which we have considered in the preceding sub­sections, are valid in the lower temperature domain, i. e., as long as dissocia­tion does not occur. Air begins to dissociate at temperatures between 1,500 K and 2,000 K, depending on the density level. In general the following holds: the lower the density, the lower is the temperature at which dissociation occurs.

If appreciable dissociation is present, the transport properties are de­termined separately for each involved species. Mixing formulas (exact, and approximate ones such as Wilke’s and other [2, 3]) are then employed in order to determine the transport properties of dissociated air.

Wilke’s semi-empirical formula, for example, reads [2]:

with

where pi, xi and Mi are viscosity, mole fraction and molecular weight of the species i, respectively, and j is a dummy subscript.

Wilke’s formula is used in aerothermodynamics with good results, also for the determination of the thermal conductivity of gas mixtures. For multi­component diffusion coefficients the available mixing formulae, [2], are less satisfactory [9].

The transport properties of gas mixtures in thermo-chemical equilibrium are always functions of two thermodynamic variables, for example internal energy e and density p.

The nowadays fully accepted theoretical base for the determination of transport properties is the Chapman-Enskog theory for gases at “low” density with extensions also for dissociated air in equilibrium or in non-equilibrium. In the methods of numerical aerothermodynamics curve-fitted state surfaces are employed, see, e. g., [10], in order to obtain in a fast and exact manner the needed data. They use extensive data bases, e. g., [11]—[13].

In general it is accepted that transport properties of multi-species air at the flow conditions considered here can be determined to a sufficient degree of accuracy [9, 14]. The situation is different with flow problems exhibiting very high temperatures, and with combustion and combustion-wake problems of hypersonic flight propulsion systems.

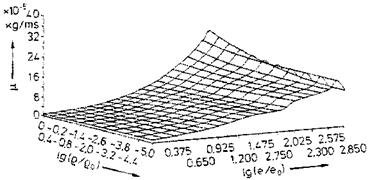
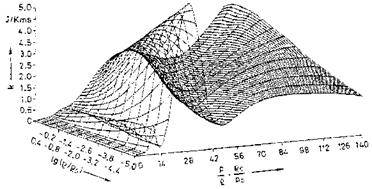
Examples of curve-fitted state surfaces of viscosity p(p, e) and thermal conductivity k(p, p/p) [10] for the typical pressure/density/internal energy range encountered by the flight vehicle classes in the background of this book are shown in Figs. 4.6 and 4.7.[31]