EQUATIONS OF MOTION OF AN ARBITRARY SYSTEM
 |
The equations of motion result from the application of Newton’s laws of motion to the material system that constitutes the flight vehicle. Consider
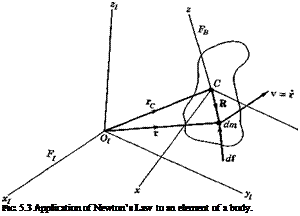
an element of mass dm, and an inertial frame of reference FT (see Fig. 5.3). (Since only one reference frame is used in the following argument, no identifying subscript is appended to the vector symbols. The subscript I should be understood.) Newton’s second law provides the equation of motion of dm, i. e.
di = r dm — v dm (5.4,1)
Here di is the resultant of all the forces acting on dm, r is its position vector, and v its velocity. In this form, the equation is valid only in an inertial frame of reference.
Taking the cross product of (5.4,1) with r yields the moment equation
r x di = r x v dm (5.4,2)
Now let the angular momentum of dm w. r.t. О be defined as
— (dh’) = (r x v r x v) dm dt
= (v x v + r x v) dm
— (dll’) = r x v dm dt
|
which is the r. h.s. of (5.4,2). We therefore have
|
where vc and ac, are respectively the velocity and acceleration of the mass center relative to Fr The integral of (5.4,1) is obtained from (5.4,8) as
![]() (5.4,9)
(5.4,9)
where f = j df is the vector sum of all the forces acting on all the elements. Since the internal forces, those which one element of the system exerts upon another, occur in equal and opposite pairs by Newton’s third law of motion, they vanish from J df: f is then the resultant external force acting on the system m. Similarly, the integral over m of (5.4,4) is simply,
G’ = – h’ (5.4,96)
dt
where G’ = j" r x df is the resultant external moment about O, and
h’ = J*r x v dm (5.4,10)
is the resultant angular momentum about O. Let

r = rc + R
as shown on Fig. 5.3. Note that from (5.4,6)
![]() J R dm = 0
J R dm = 0
Then we may expand (5.4,96) as follows:
jVc+R) x«*f=| J (rc – fE) x t dm Since rc is constant, it can come outside the integrals, to give
v dm + — Jr x v dm
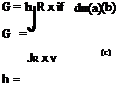 |
||
From (5.4,8) and (5.4,9) the leading terms on the l. h.s. and r. h.s. are seen to be equal, so the equation reduces to
are, respectively, the moment and angular momentum about <7. Note that (5.4,96) has the same simple form as (5.4,12) even though the former is referenced to a fixed point in inertial space, and the latter to a moving point, the mass center. This simple form does not hold, for arbitrary motion of the systems, for any moving reference point except the mass center.
Equations (5.4,9) and (5.4,12) are the two fundamental vector equations, equivalent to six scalar equations, that relate the “gross” motion of the body to the external forces that act on it. The description of the “fine” motion (distortion and articulation) requires additional equations that are given subsequently.











