Exercises
3.1 Derive (3.1,4).
3.2 Derive an expression for the elevator angle per g in dimensional form. Denote the derivatives of L and M with respect to a and q by dL/dq = Lq, and so on. There are two choices: (1) do the derivation in dimensional form from the beginning, or (2) convert the nondimensional result (3.1,6) to dimensional form. Do it both ways and check that they agree.
3.3 Calculate the variation of the control force per g with altitude from the following data. Ignore propulsion effects.
 |
 |
Geometric Data
|
bx |
—0.17/rad |
|
b2 |
—0.48/rad |
|
4 |
-0.846 |
|
CL |
0 |
|
cmq |
-22.9 |
|
1? 1 a |
-0.10 |
|
ЭеЭа |
0.30 |
|
0 |
3.4 A small manually controlled airplane has an undesirable handling characteristic—the control force per g is too large. List some design changes that could reduce it, and describe the other consequences that each such change would entail.
3.5 The range of elevator motion on an airplane is from 20° down to 30° up. Use Table
1.3 as a guide, a fellow student as a model, and a tape measure to arrive at a reasonable value for the elevator gearing ratio G.
3.6 Two airplanes are similar, but one is jet-propelled and the other has a piston engine and propeller. The thrust line in each case is well below the CG with zp! c = 0.4. The power-off pitching moment at 8e = 0 is Cm = 0.1 — 0.2 CL. The throttle is set to give level flight with CL = 0.4 and L/D =12. Consider several steady rectilinear flight conditions having the same throttle setting but different elevator settings, CL values and flight-path angles. Find dCJdCL for the two airplanes when passing through the altitude corresponding to the level flight conditions. As indicated in Sec. 3.4 and
(6.4,10) ![]()
![]()
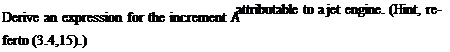 |
dCJdCL is an index of static longitudinal stability under certain conditions. Assuming that these conditions are met in this problem, how will the static longitudinal stability of the two aircraft change as the aircraft slow down?
3.8 Suppose that as a result of an accident in flight the rear fuselage of an airplane is damaged, so that the flexibility parameter k in (3.5,1) et seq. is suddenly increased. The effect is large enough that the pilot notices a loss in longitudinal stability and control. Bearing in mind that the integrity of the fuselage structure depends on the tail load L, and the stability and control on the factor in parentheses in (3.5,4), analyze how the situation changes as the pilot slows down and descends to an emergency landing. Consider two cases; (1) Cu initially positive, (2) C, t initially negative.
3.9 Derive (3.9,8). Explain clearly each step in the development and justify any assumptions you make.
3.10 ![]() Use Appendix В to determine the elevator hinge moment parameters bx and b2 for a NACA 0009 airfoil (a symmetric airfoil with a thickness-to-chord ratio of t/c =
Use Appendix В to determine the elevator hinge moment parameters bx and b2 for a NACA 0009 airfoil (a symmetric airfoil with a thickness-to-chord ratio of t/c =
0. 09). The elevator has an elliptic nose, a sealed gap and a balance ratio of 0.2. In using the curves assume that transition is at the leading edge; R = 107; tan
![]()
![]() Фтв
Фтв













