Flow-Field Modeling with Source and Vortex Sheets

The representation of low-speed aerodynamic flow-fields using source, vortex, and doublet sheets, when possible, is attractive for a number of reasons.

• In a typical aerodynamic flow with thin viscous layers, very little accuracy is lost when vorticity ш in the layers is lumped into vortex sheets 7 placed on the body and wake surfaces. This is equivalent to the usual inviscid-flow approximation. Chapter 3 examines this model’s limitations and gives modifications to greatly improve its accuracy for cases where the viscous layers are not very thin.

• Only the body surfaces and possibly trailing wake surfaces need to be geometrically defined. In contrast, directly defining a velocity field V(r) requires construction of a space-filling grid throughout the flow-field.

• Numerical panel methods, which employ the sheet representation, require roughly 1/100 fewer un­knowns than corresponding grid methods for any given level of accuracy.

• In cases where the velocity jumps aV or potential jumps Ap across the sheets are known, the source, vortex, or doublet sheet strengths can be computed immediately. The defining relations are derived in Appendix B, and restated here:

A = n ■ AV

7 = П x aV

p = Ap

2.9.1 Source sheet applications

A source sheet can be used to exactly represent the inviscid low speed flow about a non-lifting body, as sketched in the middle of Figure 2.10. The sheet is placed everywhere on the surface, which together with an added freestream defines the total velocity field.

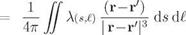
(2.64)

For the usual impermeable body, this velocity must be tangent to the body surface everywhere. Setting the field points just outside the surface at r = (s, i, 0+), this requirement is

Substitution of (2.64) into (2.65) results in

which is an integral equation for the unknown sheet strength (s, i). In practice, an approximate numerical solution can be obtained by a panel method, which discretizes the surface into a large number of small panels, and determines a piecewise-constant value of A over each such panel, such that equation (2.66) is satisfied at one control point on each panel. These A values can then be substituted into (2.64) which allows numerical calculation of the local V at any chosen point r, together with the local pressure via Bernoulli’s equation (1.109). This thus defines the flow-field. See Katz and Plotkin [4] for the extensive details.

2.9.2 Vortex sheet applications

Source sheets have the disadvantage that they cannot by themselves represent a lifting flow. This problem can be addressed by switching to vortex or doublet sheets, again placed on the body surface, as sketched on the right side of Figure 2.12. In 2D, the velocity of a vortex sheet plus freestream has the following form.

vw = F 17W y|Xr(r~f ds + V. (2.67)

Like in the source-sheet case, the requirement of flow tangency V ■ П = 0 gives an integral equation for the vortex sheet strength.

In addition, it is also necessary to impose a Kutta Condition to model the smooth flow off the trailing edge, which is what’s seen in a real viscous flow. In the vortex sheet model this requires that the summed sheet strength of the upper and lower surfaces be zero at the trailing edge.

YTEupper + ‘7TE lower 0

The solution for the unknown y(s) can be again obtained by a panel method.