Fundamental Feature of the Flow Past Finite Wings: The Vortex Sheet

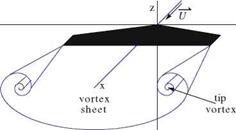
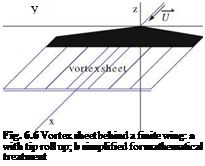
The small disturbance potential equation, governing the flow past thin wings and slender bodies, admits jump conditions which represent discontinuities in the flow. Shock waves in linearized supersonic flow are such discontinuities and correspond to jump of velocity, density and pressure across characteristic surfaces. In incom­pressible or low speed flow, shock waves do not occur. However, at all flow regimes, discontinuities of a different nature are admissible that are called vortex sheets. A vortex sheet occurs at the sharp trailing edge of a wing and trails behind it to down­stream infinity. To simplify the mathematical treatment, the vortex sheet rolling up at the edges into tip vortices is neglected. This will not affect the vorticity content of the vortex sheet, but only modify slightly its distribution in space. It has been found that this effect is of second or higher order, Fig. 6.6.

The study of the jump conditions associated with the perturbation potential equa­tion provides insight into the type of discontinuities that can be present with this flow model. First, the second order PDE is transformed into an equivalent first order system in (u, v, w) as

y

(l _ M2 – і— dv і dw _ о

l1 M0) dx + dy + dz — 0

dw dv

d — d — 0

_ dw і du __ о

dx + dz — 0

Here we have used the governing equation and two components of the irrotation – ality condition. The third component is a consequence of the other two. The jump conditions for this system read

1 — Mq) < u > nx + < v > ny + < w > nz — 0

< w > ny — < v > nz — 0 (6.11)

— < w > nx + < u > nz — 0

This is a homogeneous system for the components (nx, ny, nz) of the normal vector to the jump surface. For a non-trivial solution, the determinant must vanish, i. e.

I ^1 — Mq^ < u >2 + < v >2 + < w >2J < w >— 0 (6.12)

Two cases are possible:

(i) < w >— 0. The equation reduces to (1 — M^) < u >2 + < v >2 +

< w >2— 0. A non trivial solution can only be found if 1 — Mq2 < 0, that is if the flow is supersonic. The surfaces that admit this jump condition are shock waves that coincide with characteristic surfaces of the PDE. Note that Prandtl-Meyer expansions will be represented by “expansion shocks” in this linear theory. The flow crosses the shock surface which is not a stream surface since < w > — 0. In general < v >— 0 (except in a plane of symmetry). The component u must have a jump for a non-trivial solution, i. e. < u > — 0, which indicates that the pressure is discontinuous.

(ii) < w >— 0. The jump condition is satisfied. In general < v >— 0 (except in a plane of symmetry). The fluid is tangent to the surface of discontinuity since

< w >— 0. It is called a vortex sheet. The vortex sheet is a stream surface, not a material surface, therefore it cannot withstand a pressure difference across it. This implies that < u >— 0. In consequence, the only velocity component that has a jump at a vortex sheet is the v-component.