INERTIAL ACCELERATION

We have two particular requirements for the inertial acceleration of a particle in a moving reference frame: one is for the Fw or FB components of the acceleration of C or 0V, the vehicle mass center, and the other is for the FB components of the acceleration of a particle in arbitrary motion relative to the vehicle. Other reference frames may be of interest for application to special dynamics problems, or for the analysis of navigation and guidance systems in which expressions are needed for the outputs of accelerometers mounted on inertial platforms that are oriented in accordance to some particular navigation scheme. The two applications first mentioned above are developed here; and as a matter of interest, we give also the formulation needed for a particular navigation application.

Acceleration of G. The basic equation for the inertial acceleration of the mass center is (5.1,7), in which the moving point is 0r, in the rotating frame Fe. r’ is then the velocity of the mass center relative to Earth, which we have denoted E. We assume here, as in Sec. 5.2, that the Earth’s axis is

fixed in inertial space, and that <«> = 0. Thus the acceleration a0 of the origin of FE is the centripetal acceleration associated with Earth rotation. A numeri­cal comparison shows that this acceleration is usually negligible when com­pared with g. It is zero at the poles, and of order 1/1000 g at the equator (sea level). The same holds true for the centripetal acceleration dwr’ of

(5.1,7) —i. e. it is usually negligible. Of the two terms that remain in (5.1,7) r’ = Vе and the Coriolis acceleration is 2{ЬЕХК. The latter depends on the magnitude and direction of the vehicle velocity, and is at most 10% g at orbital speed. It can of course be larger at higher speeds. This term must therefore be kept in the mathematical model, even though it is at times negligible. Finally then, the When the atmosphere is at rest, W = 0 and the components of (5.3,11) are

= t

— V (fEw + rw)

[Note that toK and biW are both angular velocities relative to inertial space, and that the sum (rKw + r,,-) for example, is not the resultant yaw rate of Fw relative to Fj, as one might be tempted to infer from (5.3,15).]

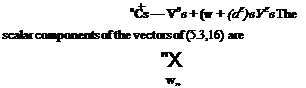For the frame FB, the same procedure yields instead of (5.3,11)

= w + (p + PEB)V – (? + W

Acceleration of a Particle in FB. A particle having coordinates (x, y, z) in FB has inertial acceleration components in the directions of the axes of FB given by (5.1,8), in which a0 is the inertial acceleration of the origin of FB and (p, q, r) are the components of ы. Since the origin of FB is the vehicle mass center then a0 = ac and its components are those given above in (5.3,18). The required equations are then obtained by substituting (5.3,18) for a0 in (5.1,8).

The Navigation Case. From the general relations already given, it is a straightforward, although tedious, calculation to derive the equations for the acceleration components aF of a moving particle. This particular set of components is that measured by an inertial navigation system in which accelerometers are mounted on a stabilized platform that is “Schuler tuned” to maintain one axis vertical, and is “torqued” to maintain one horizontal

axis directed north. In the navigation application, the accelerations of interest are very small, and are in effect integrated twice over long periods of time to give position. Thus the small centripetal acceleration [the last term of

(5.1,7) ] is not negligible, and the complete equation must be used. The acceleration of the origin of Fv (which may be taken to be the location of the inertial platform in this application) is then [cf. (5.3,8)]

= Vee – {G>B<bEkrSt)E + 2(aEEYEE (5.3,19)

where kF is a unit vector on Gzv, and the second term is the centripetal acceleration previously neglected. After transforming to Fv, i. e. aoF = L№a„s, (5.3,19) gives B

r = V*F + (&F – G>E)vEr – (G>E&EkrSl)r + 2<aErEr (5.3,20) tarv and <aEv are given respectively by (5.2,4) and (5.2,1), and from (5.3,1)

‘ SIX ‘ Sift cos X. —St

The components of the unit vector kF in Fr are of course [0, 0,1]. After substituting the above expressions into (5.3,20) and expanding the mat­rices, the following system of equations in (M, X, ft) are obtained:

a — SIX + 2MX + St sin X cos X{a>E + /і)2

a0vr = St cos Xfi + 2(a)E + fi)(Sl cos X — SIX sin X) (5.3,22)

a0zr = ~St + тг + St, cos2 X{a>E + ft?

When accelerometers provide measurements of the l. h.s. of (5.3,22), a navigation computer can in principle solve the three equations for the geocentric position (St, X, ft). For horizontal flight or when St can be ne­glected, the result is simpler, i. e.

a0^ = SIX – f St sin X cos X{wE – f ft)2 a0^ — —St cos Xja — 2(coE + {t)SlX sin X

This is a pair of equations for the latitude and longitude of the vehicle. To mechanize them for analog or digital computation, they would be more conveniently rearranged as