Small Disturbance Theories

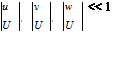Assume inviscid, steady flow past a thin wing that disturbs only slightly the incom­ing uniform flow of velocity U, parallel to the x-axis. Let (u, v, w) be the small perturbation components. The velocity vector is given by

Since the flow is tangent to the obstacle, the condition for small disturbance is that the wing or the body makes a small angle with the x-axis. In other words, the obstacle must be close to a cylindrical surface, the base surface, generated by straight lines parallel to the x-axis and touching an arbitrary curve called the base line. In the case when the curve reduces to a point, the base surface degenerates to a line parallel to Ox called the axis of the body. In the first case, the obstacle is called a thin wing. In the second case, the obstacle is called a slender body, Fig. 6.5. Slender bodies and low aspect ratio wings are the object of Chap. 7, where slender body theory will be discussed. For the rest of this chapter, we will develop the theory for thin wings of large and moderate aspect ratios.

Note that the base line can be curved. For example, it can be an arc of a circle in the (y, z) plane, centered on the z-axis and tangent to the y-axis at the origin. If a wing geometry is drawn on such a cylindrical surface, an infinitely thin wing will be defined and the wing will have curved up tips, but as such will not disturb the incoming flow.

Thickness, camber and incidence can be added to the thin wing geometry as defined above, and the same restrictions for thin airfoils apply, i. e.

The addition of thickness, camber or incidence is expected to create a small