THE OSCILLATION OF CYLINDRICAL STRUCTURES IN A FLOW

In the preceding section, it is seen that asymmetry develops itself in a flow around a circular cylinder if the Reynolds number is sufficiently

large. A lift force, perpendicular to the direction of flow, is created by the unsymmetric flow. Should the circular cylinder be stationary, there will be no exchaflge of energy between the cylinder and the flow. But, if the cylinder oscillates in phase with the lift force, the fluid will do work on the cylinder through the lift force, and energy will be extracted from the flow and imparted to the cylinder. The oscillation of the cylinder can then be built up.

Let us consider a two-dimensional cylinder of unit length supported by a spring and a dashpot (Fig. 2.5). Let the spring constant be K, the mass

Fig. 2.5.

per unit length m, and the ratio of the damping constant to the critical damping y* If the cylinder oscillates in still air, the natural frequency to0 (radians per second) will be given approximately by the equation

The equation of motion of the cylinder in a flow is then

d2x dx 1

where F(t) is the aerodynamic force per unit length acting on the cylinder, and x is the transverse displacement (perpendicular to the direction of flow) of the cylinder. Now F(t) consists of the lift force acting on the

* For a free-vibration system governed by the equation

mx + (Sac + Kx = 0 ((9 > 0)

the motion will be periodic if (S < (Scr, and aperiodic if (S > (Scr, where the critical damping f! CI is given by

(SCr = 2 VmK — 2 mco0

to0 = VKjm being the frequency (radians per second) of the system without damping.

It is often convenient to write (S as y/Scr. Then, if we divide through by m, the equation of motion can be written as

ac + 2yw0x + <о0гх – 0

cylinder due to shedding of vortices and the apparent mass force of the air

7fd^ d2x

surrounding the cylinder. The latter is equal to p where p is the

density of the air. Let us assume that the apparent mass of air is negligible in comparison with the mass of the cylinder m. (Otherwise we may simply modify m to be m’ = m + рттс12ІА.) F(t) is then regarded as the lift force alone. (The drag has no effect on the transverse oscillation.) By dimensional analysis, F(t) can be written as

F(t) = p U2CLd (per unit length of cylinder) (2)

Now the lift coefficient CL excited by the shedding of vortices can be written in the complex form

cL = Curl (3)

where о) is the frequency (radians per second) of the vortices on each side of the cylinder.[8] си is related to the Strouhal number by

w = Ukld (4)

Hence, we may write

/72-vi /fvi 1

— + 2yco0 — + u>2x = —pU2 dCL0 еш (5)

The steady-state solution of this equation is, according to § 1.8,

x(t) = Ad^1’^

where

a _ P dCL0_____________________

2mo)2 [(1 – О2)2 + (2у£ї)2]’Іг

со forcing frequency

co0 undamped natural frequency

^arctan(_^L)

The amplitude of the response x(t) is given by A, to which the stress in the spring is proportional. Now, by Eqs. 4 and 7,

„ ud

R = — v

Hence the dependence of A on U is rather complicated.

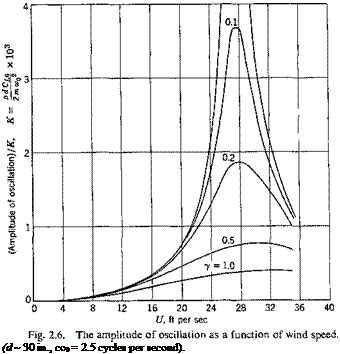Let us consider a numerical example of a pipe line with d = 30 in. and coq = 2.5 cycles per second. Then R = 16 x 103(У. Using the data given by Relf and Simmons (Fig. 2.4), we obtain the amplitude response

A as a function of U and у by substituting О into Eq. 7. The result is shown in Fig. 2.6. It is seen that maximum amplitude is reached when U is approximately 28 ft per sec or 19 mph while the frequency ratio О is approximately 1.

The calculated amplitude response near and beyond the wind speed at which the maximum response occurs is somewhat doubtful, because in that Reynolds number range the flow is turbulent, and the power spectrum of the wake is no longer a sharp line. In other words, the wake frequency is no longer sharply defined. The flow and the lift force are stochastic

processes and must be analyzed accordingly. The real response curves are probably flatter than those given by Fig. 2.6.

The value of CL0 is of the order of 0.63 if the Reynolds number of flow lies between 40 and 3 x 105.

The above calculation is based on the experimental values of к obtained on a stationary cylinder. Hence, the calculation is valid only when the amplitude of oscillation is infinitesimal. If the amplitude is finite, additional aerodynamic force associated with the shifting of the points of separation on the cylinder during the oscillation will become important. Such additional lift is, in general, a nonlinear function of the amplitude. An example of how the motion of the structure may affect the shedding of vortices and the characteristics of aeroelastic oscillations will be given in the next section in connection with the H-shaped sections.

Resonance Condition. The example given above shows that the maxi­mum amplitude of oscillation is reached in the neighborhood of Q = 1;

i. e., when the frequency of shedding vortices agrees with the natural frequency of the structure. This gives an easy rule for estimating the character of the structure as follows: Let us define a Strouhal number of the structure: .

k = (Q)

^Stru rj v-v

^max

where co0 is the fundamental natural frequency (radians per second) of the structure in still air, d is the characteristic length (here the diameter of the cylinder), and t/raax the expected maximum speed of flow (i. e., the highest wind speed). Determine the maximum Reynolds number R — t/max djv. From Fig. 2.4 find the corresponding к of the shedding vortices. Let this к be denoted by kCT; then large amplitude resonant oscillation will not occur if £stru is greater than kCI by a sufficiently large margin.

Applications to Three-Dimensional Structures. The two-dimensional model treated above may be regarded as a typical section of a three – dimensional structure. For an example of an overground pipe line, m may be taken as the mass per unit length at the center span, co0 the funda­mental natural frequency of the pipe line, and у the ratio of the actual damping to the critical damping when the pipe line oscillates in the fundamental mode. For a smokestack, the typical section may be taken at three fourths of its length above ground.

Generalization of the analysis to three-dimensional structures can be made without difficulty. The simplest approach is to use generalized coordinates and Lagrange’s equations. However, the effect of a free tip on the fluctuating aerodynamic force is both profound and difficult to predict. Rash calculations without due account of the tip-effect can be dangerous.