. THE TELESCOPE MOCK-UP
|
№ |
u>i{rd/s) |
di |
№ |
u>i(rd/s) |
di |
|
1 |
288 |
0.006 |
11 |
1162 |
0.004 |
|
2 |
536 |
0.098 |
12 |
1175 |
0.015 |
|
3 |
558 |
0.038 |
13 |
1200 |
0.005 |
|
4 |
647 |
0.003 |
14 |
1309 |
0.006 |
|
5 |
714 |
0.002 |
15 |
1329 |
0.007 |
|
6 |
799 |
0.002 |
16 |
1364 |
0.008 |
|
7 |
870 |
0.010 |
17 |
1418 |
0.009 |
|
8 |
901 |
0.011 |
18 |
1447 |
0.005 |
|
9 |
933 |
0.011 |
19 |
1563 |
0.012 |
|
10 |
943 |
0.013 |
20 |
1563 |
0.005 |
|
Figure 2.6. Flexible modes. |
This mock-up, which is used to study high accuracy pointing systems, is composed of a two axis gimbal system mounted on Bendix flexural
pivots. We more precisely focus on the elevation axis of the telescope. A 40th order identified model is available. The frequency response of the transfer function g(s), between the commanded torque and the acceleration measured on the telescope main body, is depicted in Figure 2.5. The characteristics of the 20 poorly damped modes of the model are presented in Figure 2.6.
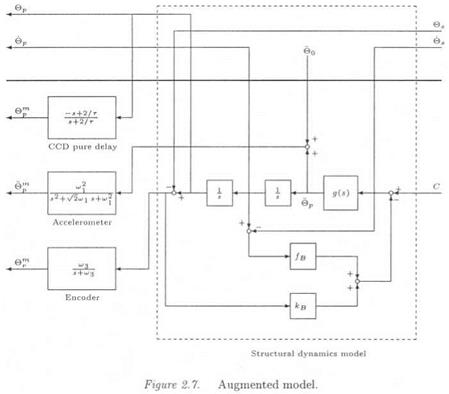
The main control design objective is the rejection of supporting vehicle disturbances. To achieve this goal, an augmented model is built on the basis of the identified model g( s) . As usually in i# or #2 synthesis, the control design objective is expressed under the standard form of Figure 2.7, as the minimization of the transfer from the disturbances (position and velocity of the supporting vehicle 6S and 6S) to the controlled outputs (position and velocity of the telescope 9P and 9P).
|
|
C represents the control input. Three measurements are available, which add sensor dynamics to the system : 0™, в™ (inertial elevation angle and angular acceleration) and 9™ ss 0P — 9S (relative elevation angle). Bendix pivots are represented by feedbacks of stiffness and friction кв and /в■ The order of the augmented system is equal to /V 6, where N is the order of g{s) (40 if the full order identified model is used) and 6 represents the 2 Bendix states and the 4 sensor states.
See (Madelaine and Alazard, 1998; Alazard et al., 1996; Madelaine, 1998) for the design of the control law. Note simply that the order of the #2 controller is 13, so that when applying this controller to the 46th full order plant model of Figure 2.7, a 59th closed loop flexible system is obtained. In this example, the issue will be to analyze the robustness properties of this #2 controller with respect to uncertainties in the natural frequencies of the bending modes (see chapter 10).