Two-Dimensional and Three-Dimensional Vorticity epresentations

The vorticity distributions in 2-D and 3-D have similarities and differences that can help explain the flow features and make connections between the two flow situations. First we look at the vortex filaments in a 2-D flow past an infinite wing and of the simplified 3-D model for a finite thin wing. In 2-D the vortex filaments are

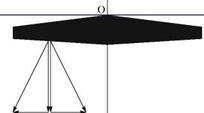
Fig. 6.7 Vortex filaments: a straight filaments in 2-D; b horseshoe filaments in 3-D

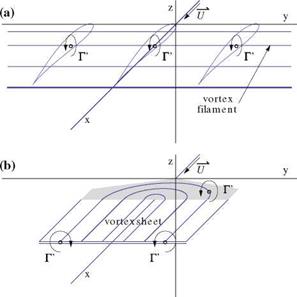
perpendicular to the plane of the profile and they carry a constant vorticity Г'(x). In 3-D, the vortex filaments have the shape of a horseshoe: they come from infinity downstream, enter the wing at the trailing edge, bend into the wing and exit at the trailing edge to trail to downstream infinity. The vorticity Г’ is constant along the filament. The part of the vortex filament inside the wing (or inside the profile) corresponds to the bound vorticity. Outside the wing, the filaments are parallel to the x-axis and the vorticity they carry is called trailed vorticity, all the way to the plane at downstream infinity called the Trefftz plane, Fig. 6.7.

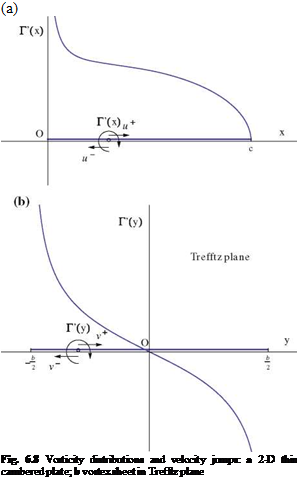
The bound vorticity inside a profile and the trailed vorticity in the vortex sheet give rise to a discontinuity in the velocity field. Consider for example a thin cambered plate in 2-D and the trace of the vortex sheet in the Trefftz plane in 3-D, Fig. 6.8.In 2-D, the vorticity along the x-axis is responsible for the jump in u across it, with u(x, 0+) = Г'(х)/2 and u(x, 0-) = —r'(x)/2. In the Trefftz plane, the situation is identical to that inside the profile in 2-D, with an infinite straight filament responsible for the jump in v across the vortex sheet, where v(<x>, y, 0+) = Г'(у)/2 and v(<x>, y, 0—) = — Г ‘(y)/2.

Note that, in general, Г'(±b/2) = ^сю, that is the flow at the edge of the vortex sheet behaves as at the leading edge of a thin plate. The velocity components v and w are infinite. Note also that the flow satisfies a Kutta-Joukowski condition at the trailing edge in 2-D and 3-D.

The circulation is the integral of the bound vorticity inside a profile according to dГ = Г’dx. At the trailing edge the value Г(с) obtained corresponds to the total vorticity inside that profile. Downstream of the trailing edge the circulation is a

function of y only, Г(y), and remains constant along the vortex filaments all the way to the Trefftz plane. This is a consequence of the pressure continuity across the vortex sheet. Indeed, < u >=< ^ >= < Ф > = ут = 0. In 2-D, for an infinite wing,

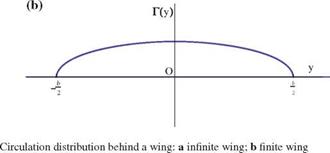
the circulation at the trailing edge, Г(y) = Г(с) is the same for all profiles, hence the velocity component v is continuous across the z = 0 plane downstream of the trailing edge. There is no trailed vorticity and no vortex sheet. Two such circulation distributions are shown in Fig. 6.9.

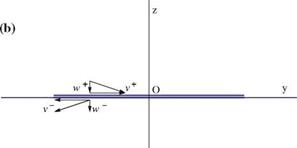
The velocity components at the trailing edge, above and below the vortex sheet of a finite wing, are depicted in Fig. 6.10. The components are continuous across the vortex sheet, except for the y-component. The same result holds at any point on the vortex sheet.

(a)

F(y)

O y

Fig. 6.9
(a)
y
v	u u	v
x Fig. 6.10 Velocity vectorjump at trailing edge: a in wing plane; b cross flow plane