TWO-DIMENSIONAL VERSION OF THE BASIC SOLUTIONS

Source. We have seen in the three-dimensional case that a source element will have a radial velocity component only. Thus, in the two-dimensional r-6 coordinate system the tangential velocity component qe = 0. Requiring that the flow be irrotational yields

[Iі{rq’y- Те И=теш~°

and therefore the velocity component in the /–direction is a function of r only (qr = qr(r)). Also, the remaining radial velocity component must satisfy the continuity equation (Eq. (1.35)):

dr r r dr

This indicates that rqT = const. = о 12л where a is the area flow rate passing through a circle of radius r, and the resulting velocity components for a source element at the origin are

_ ЭФ _ a ^r Эг 2лг

ЭФ

где

By integrating these equations the velocity potential is found,

Ф = In r + C (3.59)

and the constant C can be set to zero, as in the source potential used in Eq.

(3.19) .

The strength of the source is then a, which represents the flux introduced by the source. This can be shown by observing the flux across a circle with a radius R. The velocity at that location, according to Eq. (3.57), is o/2nR, and the flux is

a

qr2nR = —— 2 nR = a 2nR

So the velocity, as in the three-dimensional case, is in the radial direction only (Fig. 3.3e) and decays with a rate of 1/r. At r = 0, the velocity is infinite and this singular point must be excluded from the region of the solution.

In cartesian coordinates the corresponding equations for a source located

Ф(дс, z) = — in V(* – x0)2 + (z – Zof

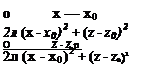at (x0, z0) are

In the two-dimensional case, the velocity components can be found as the derivatives of the stream function for a source at the origin. Recalling these formulas (Eqs. (2.80a, b)) and comparing with the velocity components results in

1ЭУ о ^r г дв 2лг

Integrating Eqs. (3.63) and (3.64) and setting the constant of integration to zero yields

Ф = (3.65)

The streamlines (Eq. (3.65)) and the perpendicular constant potential lines (Eq. (3.59)) for the two-dimensional source resemble those for the three – dimensional case and are shown schematically in Fig. 3.3a.

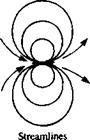
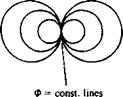
Doublet. The two-dimensional doublet (Fig. 3.7) can be obtained by letting a point source and a point sink approach each other, such that their strength multiplied by their separation distance becomes the constant ц (as in Section

3.5) . Because of the logarithmic dependence of the source potential, Eq.

(3.32) becomes

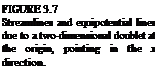ф(г).-|^ (3.66)

which can be derived directly by using Eq. (3.33), and by replacing the source strength by fi,

Э a Ф(г) = – —— lnr an 2 7t	(3.67)
As an example, selecting n in the x direction yields
ц = (ju, 0)
and Eq. (3.66) for a doublet at the origin becomes
^ и cos в ф(г, в) = ~ 2л r	(3.68)
The velocity field due to this element can be obtained by differentiating the velocity potential:
ЗФ /л cos в dr 2 лг2	(3.69)
1 ЗФ (i sin в г дв 2лг2	(3.70)

In cartesian coordinates for such a doublet at the point (jc0, z0)>

t – jU X~X° {X, Z) 2л (x – x0)2 + (z – z0)2	(3.71)
and the velocity components are
F (x – x0f – (z – z0f U 2л [(x – x0)2 +(z – z0)2]2	(3.72)
H 2(x – x0)(z – z„) Ш s — – — — 2^r [(* — x0)2 + (z — Zo)2]2	(3.73)
To derive the stream function for this doublet element, located at the origin, write the above velocity components in terms of the stream function derivatives:
ЭФ fi sin в dr 2 лг2	(3.74)
1 dW fi cos в r dd 2лг2	(3.75)

Integrating Eqs. (3.74) and (3.75) and setting the constant of integration to zero yields (see streamlines in Fig. 3.7):

(i sin в

Note that a similar doublet element where ц = (0, ц) can be derived by using Eq. (3.66) (or (3.67)),