CHENG AND DE MOOR’S METHOD
As said at the beginning of this chapter, an LFT model can be computed when the coefficients of the state space model or transfer matrix are most generally rational functions of the parametric uncertainties. The aim of this subsection is to illustrate this by detailing the method by (Cheng and DeMoor, 1994). This technique uses the fact that an interconnection of LFTs is also an LFT. The idea is to realize separately the linear and nonlinear parts of the model.
Let:
x = A(6)x + B(S)u
у = C(S)x + D(5)u (3.21)
where the coefficients of the matrices A(<5), B(6), C(8) and D(6) are rational functions of the vector 2 of parametric uncertainties. As in the previous section, the above equations can be rewritten as:
р(8) = ро + ‘£ъш
![]()
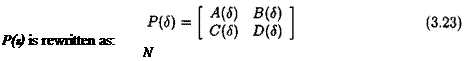 |
3=1
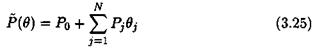 |
where the /#)’* are scalar rational functions of <5. Consider then the fictitious matrix Р(в):
 |
Using the method of the previous section, it is easy to realize the matrix m as an LFT F (Rt. 0)} where 0 — cHag^Ojlqf and ({j is the rank of matrix
On the other hand, the scalar rational functions fj{8) are realized as elementary LFTs fj(S) — Fi(Hj, Aj), where Aj = diag( SiIqid) is a diagonal matrix containing possibly repeated real scalars Si (the number qitj of repetitions of the scalar Si in the model perturbation Aj obviously depends on the structure of the scalar rational function fj(S)). To
illustrate this in a simple way, let:
and let Ді = 8. Then:
Any rational first order function can thus be realized under the above LFT form.
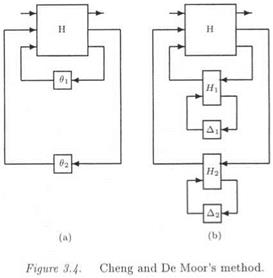
Remember now that 9j = fj{8), so that an LFT model of the matrix P(8) can be computed as the interconnection of the LFT P(6) = F[(H, 0) with elementary LFTs 9j = fj{8) = Fi(Hj, Aj): see the example of Figure 3.4, in which two scalar rational functions 6 = f(8) and 02 = f2(8) are considered.
The method is thus conceptually simple, even if a large number of elementary LFTs is possibly to be handled in practice. The approach moreover proves that an LFT model can be obtained in the very general case of coefficients of the state space model or of the transfer matrix, which are rational functions of the parametric uncertainties. Nevertheless, the method does not give (at least a priori) the minimal size LFT model.











