. Design of an Ideal Wing
The ideal wing is a wing that has an elliptic circulation or loading.
where Г0 is the root circulation to be selected. The question at hand is the following: How to design the wing so that the elliptic circulation is obtained at a given CL? As we shall see, in inviscid flow, there is an infinite number of wings that will produce
the target circulation. They differ by chord, camber and twist. Consider the Prandtl integro-differential equation, specialized to the case of ideal wing loading
Г(y) = nUc(y) {a – a0(y) + at} (6.63)
where a is the geometric incidence and at the constant induced incidence corresponding to elliptic loading Г(у) = Г0л/1 – (2y/b)2. One recalls that a0(y) = – (t(y) + 2d(y)/c(y)).
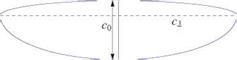
The simplest design is one in which the twist is zero, t(y) = 0, and the relative camber is constant, hence a0(y) = const. In this case, the bracket term is constant and the design is obtained with an elliptic chord distribution c(y) = с0л/1 – (2y/b)2. The root chord, aspect ratio and geometric incidence, can be found to be
Here we have made use of the area of an ellipse, S = | bc0. However, such a wing will develop an elliptic distribution of circulation at all incidences since it is easy to see that at a different incidence в
where we have used the Fourier expansion of the circulation and the identity sin t = л/1 – (2y/b)2. The two Fourier series will be equal if only if
2п(в – a0)
A1 = 2-, A2 = A3 = •••= An = 0, n > 2 (6.66)
пШ (1 + Ar)
proving that the circulation is elliptic at the new lift coefficient
Cl (в) = nARA1 = 2 (в – a0) (6.67)
l1 + AR)
Such a planform corresponds to the WWII Spitfire airplane unswept wing shown in Fig. 6.20.
Another design, which is attractive for ease of construction of small remote control airplanes, consists of a constant chord wing. The integro-differential equation of Prandtl now reads
Г(y) = nUc {a – a0(y) + at} (6.68)
where c is the wing chord and at the constant induced incidence corresponding to elliptic loading. Solving for a0(y) and letting AR = b/c yields
 |
|
 For simplicity, assume that the relative camber is constant and that the twist is a function of y. One finds
For simplicity, assume that the relative camber is constant and that the twist is a function of y. One finds
But, since without restriction, one can choose t(0) = 0, this determines the angle of incidence at design Cl
![]()
![]()
(6.72)
The rectangular wing requires an elliptic washout with a tip twist of -2Cl/п2. If this twisted rectangular wing operates at an incidence в, different from the design incidence a, the circulation is no longer elliptic and is given by
2Cl ^ sin ив ^
Г[y(ff)] = nUc в — a + г sin в — nAn = 2Ub An sin ив
п2 sin в
n=1 n=1
(6.73)
A1 is equal to the new value Cl (в)/(nAR), unknown at this stage, and the other coefficients need to be calculated using the orthogonality property. For example, multiplying both hand-sides by sin в and integrating on [0, п] gives a first relation between the Fourier coefficients (note that we only consider the odd modes for reason of symmetry)
TO
y^A2p+1 = в — a (6.74)
p=1
It seems likely that the solution will involve the infinite series of coefficients. A numerical solution is the best way to obtain the value of Cl(в).
Clearly, other designs are possible with different distributions of twist, camber and chord.











