DISCUSSION OF THE SYSTEM OF EQUATIONS

We have presented in the preceding sections a large number of complicated coupled equations that describe the kinematics and dynamics of a vehicle in flight over a spherical rotating Earth. (The student may be forgiven if he is slightly bewildered by them at this point!) Our purpose here is to evaluate these equations, show the relationships between them, and present the essential structure of the system.

Much of the complexity has resulted from the inclusion of the rotation of the earth (the to® terms) and its curvature (the to® terms) in the mathe­matical model. We have already shown (Sec. 5.3) that the centripetal acceleration associated with ыЕ is usually negligible, and that the Coriolis acceleration is small but not quite negligible. To gain further insight into the to® and to® terms we look at the z component of the force equation for horizontal flight on the equator. Thus with 6W = <f>w = 0, (5.5,8c) gives

-L + TZw + mg = – mV(qEw + qw) (5.7,1)

With tpw = 90° for eastward flight and Я = 0, (5.3,14) and (4.5,4) yield

qEw = – со® (5.7,2)

Since the Euler angles are constants, then from (5.2,8) Pw — Qw — ^W — and from (5.2,10)

qw=-(mE+fi) (5.7,3)

From (5.3,5), pt = Vj&, so that finally (5.7,1) becomes

—L + TZw + mg = mV^2wE +

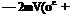
mV2

The first term on the r. h.s. is the Coriolis force due to Earth rotation, and when V equals orbital speed (about 26,000 fps) amounts to about mg. The second term is due to Earth curvature (in the “flat” Earth approxi­mation 0t = oo and this term vanishes), and at orbital speed makes up the balance, about 90 %, of mg. [Note that F is speed relative to not relative to Fj, and that the exact form of (5.7,4) would have the additional small term –тМ(ош% on the r. h.s.] Both terms on the r. h.s. of (5.7,4) increase with speed, the first linearly, the second quadratically, and each amounts to 1 % of the weight when the speed is about of orbital speed, i. e. about 2600 fps for atmospheric flight. This speed therefore seems a useful boundary below which both ыв and wF can be neglected, and above which they should be included for accurate results. It corresponds to a Mach number of about 2% to 3, depending on altitude, so that at low supersonic speeds, as for first generation supersonic transports, these terms are just marginally small— perhaps not quite negligible for range calculations. For all high supersonic speeds and hypersonic speeds they would be of increasing importance.

The preceding argument, being based on the force equation of motion, has validity only for trajectory calculations, i. e. for calculations of the flight path. When the problem of interest concerns attitude dynamics, i. e. the relatively rapid rotational motions of the vehicle relative to Fr, the situation is quite different. For then and coF can be important only if they are appreciable compared to to (greater than 1% say). Now mB m 7 x 10“5 rad/sec is extremely small compared to most technically important vehicle rotations, and wr has a maximum value at orbital speed of about 10-s rad/sec which is also negligible in this context. Hence both <aE and toF terms are normally negligible insofar as the moment equations are con­cerned.

Two alternatives have been presented for the dynamical force equations: in wind axes and body axes. Both are used in current practice, and there are no overriding advantages for either system. The wind-axes form is gener­ally more convenient for trajectory analysis, in which the attitude of the vehicle is prescribed a priori, and the moment equations are not used at all. For combined trajectory and attitude motions, either a “mixed” form of the equations, or the body-axes form, is normally employed. In hovering flight, when V — 0, and the angles oc and (j are not defined, the body-axes form is virtually mandatory. It is convenient to use a particular mixed form of the force equations for the analysis of small perturbations from a steady reference state (see Sec. 5.10).

On the other hand, there is only one reasonable choice for the moment equations. Only in FB is F constant for a rigid body. To use any other reference frame adds unnecessary complication.

Little has been said in the foregoing sections about the aerodynamic forces and moments that appear in the equations v(D, C, L, and T) in (5.5,8), (X, Y, Z) in (5.6,2), and (L, M, N) in (5.6,8). These depend on the local ambient density, the motion of the vehicle relative to the atmosphere, and on nonautonomous control inputs. Thus for a rigid vehicle, they are functions (more exactly, functionals, see Sec. 5.10) of p{&) the density, of (F, ax, /3), or (u, v, w), of (p, q, r),f and of a set of control variables. There are other ways, besides its appearance in p, in which the altitude (i. e. 1%), can occur as a nontrivial independent variable in the equations. One is when there is a wind gradient with height, e. g. WT(Sf), and another is when the vehicle flies close to the ground, so that there is a “ground eflect” on the aerodynamic field of the vehicle. In the latter case the aerodynamic forces can be very strong functions of height. A third case is when the gravitational inverse square law is included, i. e. g = g(3%). For near-orbital velocities at very high altitudes, it has been shown (ref. 5.4) that this refinement is necessary.

The structure of the mathematical system for a rigid vehicle (Jf = 0) in the more general high-speed case, and the interrelations among the variables, is displayed in Figs. 5.4 and 5.5. Each set of scalar equations is regarded as a subsystem that produces three dependent variables as outputs. The inputs are the quantities needed to calculate the outputs from the given equations. All the quantities shown immediately to the right of the square blocks can be found by algebraic solution of the equations. The aerodynamic terms in the force and moment equations have all been replaced by the state variables of which they are functions, and control forces and moments. On checking, the reader will find that all the autonomous variables needed as inputs on the left-hand side are available as outputs on the right-hand side.

To recapitulate, the mathematical models described by Figs. 5.4 and 5.5 are subject only to the following assumptions

(i) The Earth is a sphere rotating on an axis fixed in inertial space, and g is a radial vector.

(ii) The centripetal acceleration associated with Earth rotation is neglected.

(iii) The atmosphere is at rest relative to the Earth.

(iv) The vehicle is a rigid body.

None of these restrictions is made from any fundamental necessity, and any of them may be removed when the application requires it, at the cost of additional complexity.

t Actually the angular velocity of the vehicle relative to the atmosphere is to — to®, and it is the components of this vector, not (p, q, r), that strictly speaking should be used in the calculation of aerodynamic forces and moments. However to® is so small that in the majority of applications no significant error is incurred by neglecting it.

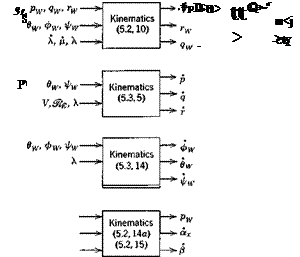Fig. 5.4 Block diagram of equations for rigid vehicle. Spherical rotating earth. Combined wind and body axes.