DIVERGENCE OF AN IDEALIZED CANTILEVER WING
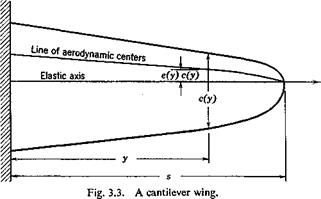
Consider an idealized unswept cantilever monoplane wing which has a straight elastic axis normal to a fuselage that is fixed in space, as in a
* This shows that, although Eq. 7 gives a finite value of the torsional deflection when the speed of flow exceeds the divergence speed, that equilibrium position is unstable. Note that the equilibrium value of в when q > qaiv is greater than a in magnitude and opposite in sign; i. e., the wing twists to opposite direction of a.
wind-tunnel testing. For such a wing the action of a general distributed load can be considered as produced by a distributed load acting through the elastic axis and a distributed twisting moment about the elastic axis. The former produces pure bending which does not affect the angle of incidence, whereas the latter produces rotation of the sections about the elastic axis.
The aerodynamic lift acts through the line of aerodynamic centers. The moment about the aerodynamic centers does not change appreciably with the angle of attack and can be neglected. Let L'(y) be the lift per unit span and ce the eccentricity of the elastic axis from the aerodynamic center (positive when the elastic axis lies behind the latter). Then the aerodynamic moment about the elastic axis is L'(y)c(y)e(y) per unit span.
The equation of divergence for a wing as shown in Fig. 3.3 can now be
|
|
derived. The fuselage of the airplane is assumed fixed in space. At the critical divergence speed, the aerodynamic moment about the elastic axis just balances the elastic moment due to twisting. For the first approximation, let us make the strip assumption that the aerodynamic lift on a chordwise strip, of width dy, due to a change of angle of attack U(y), is given by
L'(y) dy = q c(y) dy • a 0(y)
where a is the lift-curve slope corrected for aspect ratio.* The aerodynamic moment about the elastic axis is therefore
M'(y) dy = qa e(y) c%y) 0(y) dy (1)
If G(x, y) represent the influence function for wing rotation at x about the
* To account for the finite span effect, a should be corrected for the aspect ratio, as given by Eq. 15 of § 1.5 et seq.; see also § 4.3. With this correction, the resulting qai is quite accurate. Cf. Miles.3-12
 |
elastic axis due to a unit couple at y, then, the wing being in static equilibrium, the total angle of rotation 6(x) at x is
Note that Eq. 3 is satisfied only at the divergence speed, because at other speeds the wing will not be in static equilibrium if it is displaced from an equilibrium configuration, and inertia forces must be considered. This fact is indicated by writing qdlv instead of q in the equation above.
Differentiating Eq. 3 with respect to x and substituting Eq. 5, we obtain
Multiplying both sides of Eq. 6 by GJ(x) and differentiating once, we obtain
![]() GJ(x) j = – qdiv a e(x) c2(x) d(x) (7)
GJ(x) j = – qdiv a e(x) c2(x) d(x) (7)
The boundary conditions for Eq. 7 must correspond with Eq. 4; these are
d(x) = 0 when x = 0
![]() dO(x) „ ,
dO(x) „ ,
—-— = 0 when x = s dx
Equation 3 or Eqs. 7 and 8 are the fundamental equations for divergence of the idealized wing specified above. The simplification introduced by
choosing the elastic axis as a reference line for measuring the moment and twisting of the wing should be noted. If an arbitrary line is chosen as a reference line, and the aerodynamic action is resolved into a lift force acting through this reference line and a moment about it, the change of angle of incidence of the wing would have to be expressed by two influence functions: one giving the rotation at x due to a unit force at у acting on the reference line, and the other giving the rotation at x due to a unit moment at у about the reference line. The final result is equivalent to the above equations. Therefore, whenever an elastic axis can be defined and is a straight line, its use as a reference line simplifies the derivation. In general, however, for aircraft structures an elastic axis may not be easily defined because of the effect of sweep angle, cutout, or restrained warping; then the use of an arbitrary reference line together with the corresponding influence functions may become imperative. These influence functions may be computed by more advanced structural theory or by experiments.
Note further that, if the wing aspect ratio is small, or if the deformation in the root region of a swept or a delta wing is aerodynamically important, the chordwise sections may not be considered as rigid. Then it is no longer pertinent to speak of the “rotation” of the wing sections. The deformation would have to be specified by influence functions describing the deflection surface of the wing due to a unit force or moment, and the aerodynamic forces would have to be computed by the “lifting-surface” theory. In such complicated cases the formulation of the problem in the form of integral equations in terms of influence functions is still straightforward, whereas a formulation in the form of differential equations may become very cumbersome. These more general cases will be discussed later.
The assumption of a fixed fuselage may be removed by allowing proper rigid-body rotation of the entire airplane. Such a refinement generally causes only a slight correction on the divergence speed.
Return now to the idealized case, and consider Eq. 3. An obvious solution is the trivial one: 6 — 0. Then the wing is not twisted at all. In general, this is the unique continuous solution.* However, for particular discrete values of the parameter q, there may exist some nontrivial solutions. Such particular values of q are called the eigenvalues (or characteristic values) of the integral equation. The corresponding solutions are called the eigenfunctions (or characteristic functions). Since Eq. 3 is homogeneous in 6(y), the absolute magnitude of the eigenfunction is undefined. If 6(y) is a solution of Eq. З, кв(у) is another solution, where
* The requirement that the solution 0(y) should be continuous in the range 0 < у < s is imposed by physical reasons.
к is any constant. 6(y) is said to be normalized when some definite rule is specified so that its absolute value can be determined.
The physical meaning of the existence of eigenfunctions is that wing torsional divergence becomes possible when the dynamic pressure reaches certain critical values. The smallest positive eigenvalue is the critical divergence pressure which has engineering significance. For q less than the smallest eigenvalue, a disturbed wing is stable, whereas, for q greater than that eigenvalue, a disturbed wing is unstable (cf. §§ 6.3-5). Since q = pU2 is a nonnegative quantity, a negative eigenvalue, if it exists, has no physical significance. If all eigenvalues are negative, the wing is stable, and neutral equilibrium in a disturbed position is impossible.
The solution for a rectangular wing can be obtained easily, provided that the torsional stiffness GJ, the chord length c, and the eccentricity e are constant across the span. In this particular case Eq. 7 becomes
d26
(9)
where
/л2 = -^jaec2qdiv (10)
The general solution is
в — A sin /их + В cos рас (11)
where A and В are arbitrary constants which must be determined from the boundary conditions (Eqs. 8). The first condition requires that
5 = 0 (12)
and the second condition requires that
A/и cos /us = 0 (13)
Two obvious solutions of Eq. 13 are A = 0 and /и = 0. But both lead to the trivial solution 6(x) = 0. The nontrivial solutions are, therefore, possible only when /и assumes the special values for which
![]() cos /us = 0
cos /us = 0
i. e., when
іМ=±(2и+1)| (и = 0,1,2,- • •) (15)
The /и given by Eq. 15 are the eigenvalues of the differential equation 9 with the boundary conditions 8. The corresponding eigenfunction A sin /их can be normalized by taking A = 1.
|
*"v 4 aech* The lowest critical speed t/div is _ 7Г / GJ dlv cs 2pae |
 |
Hence, by Eqs. 10 and 15,
Now the same angle 012 can be produced by a moment Mx acting at the section 1, if Mx is determined from the equation
012 =
where an is the influence coefficient of angle of rotation at 1 due to a unit moment at the same section. Comparing the above equations, we see that
Mx = ^ M2 (2)
°n
When a distributed twisting moment acts on a wing, the total rotation at section 1 can be obtained by replacing the moments acting at other sections by fictitious moments acting at section 1, according to the rule given by Eq. 2.
By applying this result to the idealized cantilever wing of § 3.2 (Fig. 3.3), it is seen that the angle of rotation produced at a reference section у — r by the moment L’ce dy, acting on an element dy located at y, is equal to the angle caused by a moment
— L’ce dy a„
acting at the reference section itself. The total angle of rotation of the reference section can then be obtained by computing the angle of rotation caused by a fictitious concentrated couple of magnitude
Г ^ Idee dy
Jo arr
acting at the reference section.
According to Maxwell’s reciprocal theorem, ary = ayr. But ayJarr is precisely the ratio of the angle of rotation at у to that at r due to a unit couple acting at r. This is known for a semirigid wing, since avrlarr = f(y)lf(r), and the function f(y) (cf. Eq. 1) is assumed to be known and invariant. Hence, as far as the rotation of the reference section is concerned, the distributed load over the entire wing can be replaced by a single couple acting at the reference section, of magnitude
P-^ L'(y) c(y) e(y) dy (3)
Ju /(r)
By strip assumption, writing L'(y) = qcafJ, we obtain the representative concentrated couple at the reference section:
Г* fHv)
Ma = q(J0a cfy) e(y) dy
Jo J(n
 |
|
At the critical-divergence condition, this couple is balanced by the elastic restoring moment. Let К be the stiffness constant of the wing defined by the ratio
The elastic moment corresponding to the angle 6(r) — 0of(r) at the reference section is
![]() Me = K6af(r)
Me = K6af(r)
Hence the critical condition Ma = Me yields the following equation for the determination of qdiv:
Consider again the rectangular wing for which c, a, and e are constant along the span. Let the reference section be taken at the wing tip where у — s, and let the semirigid mode of the wing be defined by the function
![]()
Л’) = * ini
The stiffness К in this particular case is
 K =
K =
Hence,
Я&у
Note that the qdlv so obtained does not agree with the exact solution, even though the assumed mode J{y) is exact. This is caused by the incompatibility between the assumed mode (Eq. 8) and the deflection mode of the wing under a concentrated torque at the reference section, from which К is derived.
On the other hand, if the semirigid mode of the wing is taken as*
![]() (П)
(П)
and the reference section is again taken at the wing tip, then Eq. 7 gives
Hence we obtain, for a rectangular wing,
![]()
![]() _ 3 GJ
_ 3 GJ
<7dlv " aecV
The exact formula (Eq. 17) of § 3.2 gives
_ 7T2GJ ^div 4aec2s2
The dynamical pressures found by these three methods are in the ratios
7Г2
2:—: 3. The fundamental divergence speeds are approximately in the
ratios 0.9:1:1.1. The divergence speed found by the semirigid assumption Eq. 8 is about 10 per cent too low, whereas that found by the assumption Eq. 11 is about 10 per cent too high.
The stiffness constant К may be measured in practice by applying a torque on the wing at the reference section and measuring the angle of rotation. It is perhaps needless to remark that the deflection pattern obtained in this experiment (a concentrated torque) may be different from the assumed divergence mode.