Evaluation of the Angular Momentum h

We shall want the angular momentum components in FB. Now

So in FB we have

(4.3,1)

where

0 – z у r B= z 0 – x _-y x 0

Let the angular velocity of the airplane relative to inertial space1 be

<»B = [p 4 rf

where p, q, r are the rates of roll, pitch and yaw respectively (see Fig. 1.6).
Now the velocity of a point in a rigid rotating body is given by2

VB = Ve + taBrB (a)

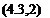
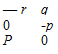where

hs = J fB(VB + coBrB)dm

= J rBB dm + J rBa>BrB dm

fe dmj VB + j rB(bBrB dm (4.3,3)

The first integral in (4.3,3) vanishes since the origin of г is the CG. When the triple matrix product of the second integral is expanded (see Exercise 4.2) we get the result for hB: hs ” IBMB (4.3,4) where " lx ^xy -hz Ifl = ^ XX Is -1, (4.3,5) L-/w ~hy h J and

Ix = j (y2 + z2)dm; Iy = J (x2 + z2)dm; Iz = j (x1 + y2)dm

(4.3,6)

hy = A t = {•*>’ dm Ixz = ]:x = f xz dm; Iyz = /:v = f yz dm

Ifi is the inertia matrix, its elements being the moments and products of inertia of the airplane. When the xz plane is a plane of symmetry, which is the usual assumption, then

^xy A 0

and the only off-diagonal term remaining is If the direction of the x axis is so cho­sen that this product of inertia also vanishes, which is always possible in principle, then the axes are principal axes.

‘Since there is no need to use the angular velocity relative to any other frame of reference the distin­guishing superscript E is not needed on at.

2See Appendix A.6.