Excitation Light

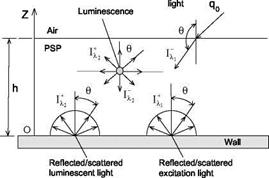
We consider a PSP layer with a thickness h on a wall, as shown in Fig. 4.2. Suppose that PSP is not a scattering medium and scattering exists only at the wall surface. When an incident excitation light beam with a wavelength Я2 enters the layer, without scattering and other sources for the excitation energy, the incident light is attenuated due to absorption through the PSP medium. In plane geometry where the luminescent intensity (radiance) is independent of the azimuthal angle, the intensity of the incident excitation light with Я can be described by

where Ix is the incident excitation light intensity, i = cos в is the cosine of the polar angle в, and px is the extinction coefficient of the PSP medium for the

incident excitation light with Л1. The extinction coefficient PXi = єх c is a

product of the molar absorptivity sx and luminescent molecule concentration c.

Again, note that the spectral intensity is defined as radiative energy transferred per unit time, solid angle, spectral variable and area normal to the ray (units: watt-m-2- sr-1-nm-1). The superscript ‘-‘ in I – indicates the negative direction in which the light enters the layer. The incident angle в ranges from ж/2 to 3 ж /2 (-1 < fi < 0) (see Fig. 4.2).

Incident excitation Fig. 4.2. Radiative energy transports in a luminescent paint layer

For the collimated excitation light, the boundary value for Eq. (4.1) is the component penetrating into the PSP layer,

I–i (z = h) = (1 – Pa/p )qo Exі (Xі)S(i – iex), (4.2)

where q0 and Ex (X1) are the radiative flux and spectrum of the incident

excitation light, respectively, pf is the reflectivity of the air-PSP interface, pex is

the cosine of the incident angle of the excitation light, and S(p) is the Dirac-delta function. The solution to Eq. (4.1) is

I-1 =(1 – p71)qoEh(Xi)8(i-iex)exp[(i)(h-z)]. (-1 <i<0) (4.3)

This relation describes a decay of the incident excitation light intensity through the layer. The incident excitation light flux at the wall integrated over the ranges of в from either ж to ж/2 or ж to 3 ж /2 is

С 0

q~xjz = 0) = – J 11-I(z = 0) ц dn = Cd (1 – pfp )qo Eh(X 2),

where Cd is the coefficient representing the directional effect of the excitation light, that is,

Cd = – Цех exP( p, h/Цех) . (-1 < Цех < 0) (4.5)

When the incident excitation light impinges on the wall, the light reflects and re-enters into the layer. Without a scattering source inside PSP, the intensity of the reflected and scattered light from the wall is described by

dl+

Ц-Z – + Pk1!: = 0 , (4.6)

where 1 + is the excitation light intensity in the positive direction emanating from the wall. As shown in Fig. 4.2, the range of u is 0 < ц < 1 (0 < в < n/2 and – n /2 < в < 0) for the outgoing reflected and scattered excitation light. The superscript ‘+’ indicates the outgoing direction from the wall. For the wall that reflects diffusely, the boundary condition for Eq. (4.6) is

where p’WPi is the reflectivity of the wall-PSP interface for the excitation light. The solution to Eq. (4.6) is

Cd P7p(1 – p? I)q0EXiai)exp(-pjLiz/ri. (0 <ju< 1) (4.8)

At a point inside the PSP layer, the net excitation light flux is contributed by the incident and scattering light rays from all the possible directions. The net flux is calculated by adding the incident flux (integrated over в = ж to ж/2 and в = ж to 3ж/2 ) and scattering flux (integrated over в = 0 to ж/2 and

в = 0 to – ж/2). Hence, the net excitation light flux is

p 0 p 0

(q>. 1 )net =- 2 J i 1 – ц Лц – 2 1 + цФ

= Cd(1 – pfp )q0 E, 1 (11)[ exp (-fix 1 z/цех) + PWP exp (-3fixt z/2)].

Note that the derivation of Eq. (4.9) uses an approximation of the exponential integral of third order, E3(x) = (1/2)exp(-3x/2).