Far-field effect of lift’s pitching moment

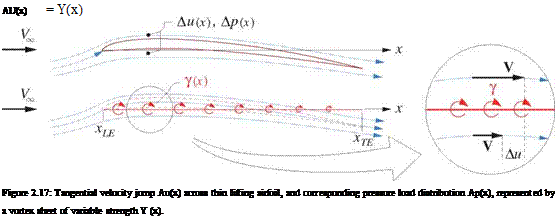Again following the thin airfoil theory model of Appendix D, the lift distribution on a thin cambered airfoil can be represented by superimposing the freestream with a vortex sheet placed along the chord line. As shown in Figure 2.17, this results in a jump in tangential velocity equal to the local sheet strength.

The corresponding pressure jump from Bernoulli’s equation is

Ap(x) = Іp [(Ко + Au/2)2 – (Ко – Au/2)2 ]

= pV, AU

= pV, Y (2.90)

which is in effect a local Kutta-Joukowsky relation. The pitching moment/span of the airfoil about the origin, defined positive nose up, is then obtained by integrating this loading with the moment arm —x.

rxTE (‘ xTE

M0 = —Ap x dx = pVo —Y x dx (2.91)

xLE xLE

From the Kz definition (2.83), with A = 0 for this case, we also have

xte

kz = —Y x dx (2.92)

xLE

where again x has been used for both x’ and s. Comparing (2.91) and (2.92) gives the z-doublet in terms of the pitching moment/span, or equivalently in terms of the pitching moment coefficient cm0 about the origin.

Hz = ^7- = 7C2 Ко Сто (2.93)

pV, 2

It’s important to note that M0 is defined about the origin of the far-field coefficient integrals (2.74)-(2.77). This is also the same location that is used to place the far-field singularities, and in particular the vortex. If a moment M^ef about some other location xref is to be used to calculate Kz, it’s necessary to derive the equivalent M0 from it by using the moment-reference shift relation.

Mo = Mr’ef – XrefL (2.94)

or cmo = cmref – °^-ce (2-95)

This M0 or cm0 can then be used to obtain kz from (2.93) as before.

2.11.3 Doublet orientation

The x and z doublet expressions (2.89) and (2.93) have been derived for the case where the freestream is along the x axis. For the more general case where Vo has an angle a relative to the x axis, these doublet expressions actually give the streamwise and normal doublets relative to the freestream direction.

K8 = V^A^l + ^-J (2.96)

Kn = ^c2I4cmo (2.97)

The corresponding cartesian kx and kz are then obtained from these by a rotation transformation.

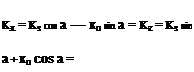u w

oo oo

Kstz—– Kn~F~ (2-98)

wo uo __

K’S-^—– h Kn-— (2.99)

In general, a doublet strength is a vector к whose components depend on the orientation of the chosen coordinate axes. These components also obey the usual transformation relations due to axes rotation.