Incompressible Flow Over Moderate Aspect Ratio Wings: The Vortex Lattice Method

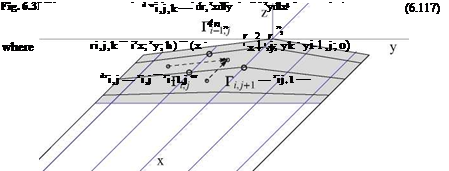
In incompressible, inviscid flow, for aspect ratio wings which are less than 7, the Prandtl lifting line theory is extended to a lifting surface theory, the vortex lattice method. For the lifting problem, consider an infinitely thin wing of equation z = f (x, y) at incidence a. The wing surface is covered with a mesh that conforms to the wing projected planform in the (x, y) plane. At the mesh node one defines the circulation Г, = r(xij, y,). Along the edges, the circulation is either zero, at leading edge and tips, or corresponds to the total bound vorticity for that cross­section inside the wing Г(у) = Г[xte(y), y], at the trailing edge. The distribution Г(y) is then carried, without alteration, along the vortex filaments to the Trefftz plane as trailed vorticity. To avoid difficulties with the singular integral, the vortices are placed between the control points as shown in Fig. 6.31.

The Biot-Savart law is used to calculate the components of the induced velocity at the interior control points due to the bound and trailed vorticity. For the bound vorticity, consider one of the two types of small, oriented elements of vorticity dli j = {dlx; dly; 0} = dli— 1 j between control points (i — 1, j) and (i, j) or dl, = dli;.+1 between points (i, j) and (i, j + 1). The induced velocity at point Mk = (xk, yk, 0) of the wing is given by

Vi, j,k — (xk – xh}+1; yk – yl ]+1; °)

The contribution to the z-component reads

The semi-infinite vortex filaments lj also contribute with the trailed vorticity to the z-component at all interior points as dwj, k. The tangency condition is enforced at the interior control points k

The Kutta-Joukowski condition is satisfied at the trailing edge by applying a parabolic extrapolation of the circulation that satisfies — 0, as was done in 2-D. Accounting for the boundary conditions mentioned above, there are as many equations as there are unknowns Г,. The linear system can be solved by relaxation. The result is the circulation at the trailing edge, r(y), that determine the lift and

induced drag of the thin wing, using the general formula derived earlier. More details on the vortex lattice method can be found in Chap. 10 on wind turbine simulation with the vortex method.