Nonlinear Lift Curve and Viscous Correction

A viscous correction can be added to the drag evaluation given by the lifting line method, by using a nonlinear viscous polar for the profiles. The viscous polar, from experiments or from the two-dimensional solution of the Navier-Stokes equations, typically displays a maximum lift coefficient at the incidence of stall a. cimax. The numerical solution of the lifting line problem becomes highly nonlinear in the vicinity of aClmax, due to the existence of two or more incidence values for a given lift coefficient Cl < Clmax. The method proposed by JJC [6], consists in adding an artificial viscosity term to the governing equation, whose role is to select the correct solution of the nonlinear problem. Lets consider the inviscid flow problem in which the lift curve presents a maximum at some value of incidence.

The governing equation for a nonlinear lift curve C; (a) reads

a – a0(y) + arctan

(6.104)

Newton’s method is used to linearize locally, at control point j, the change in circulation

where the change of effective incidence is expressed using the discrete formula for the downwash

and

where ш is the relaxation factor and Arj = Гп+1 – Гп. Note that aj < 0, so that, the second term in the bracket in the l. h.s. is positive as long as the lift slope is positive, and the solution can be over-relaxed. When stall has occurred on part or the whole wing, the term in the bracket changes sign and the algorithm for the circulation will no longer converge. The equation is modified with the addition of an artificial viscosity term in the r. h.s., which also contributes to the coefficient of Ar, to counterbalance the negative coefficient. The iterative algorithm now reads

where the artificial viscosity coefficient vj is given by

Under-relaxation is necessary (w < 1) when separation occurs.

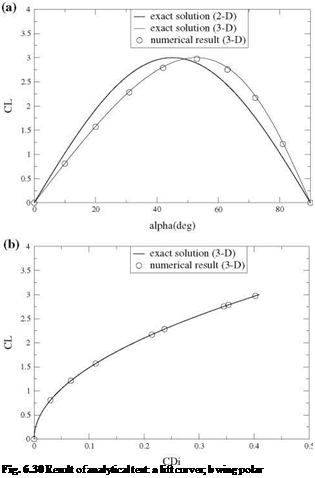A simple test case, for which an exact solution of Prandtl lifting line theory can be obtained, corresponds to the elliptic loading. Consider a wing of elliptic planform and of aspect ratio AR = 7, that has no twist and no camber. The two-dimensional lift curve is given analytically by

Cl (a) = Cimax sin 2a (6.111)

The maximum lift is obtained at a = n/4. Only the first Fourier mode is present in the solution, and the downwash is constant ww/U = —A1. The governing equation reduces to

21 (y) ww

Cl(y) = = Cl = nARA1 = Cimax sin 2a + 2 arctan – , ^

Uc(y) V U )

A1 = Cimax sin (2a — 2arctanA1) (6.112)

nAR

This last equation is solved iteratively, using Newton’s method to give Ai = Ai(a). Hence the wing lift is obtained as CL(a) = nARA1(a). Here we have chosen Clmax = 3. The inviscid nonlinear lift curves and wing polar are shown in Fig. 6.30. The numerical solution matches the exact solution very well.