Orientation and Position of the Airplane

The position and orientation of the airplane are given relative to the Earth-fixed frame Fe. The CG has position vector rc (see Fig. 4.1), with coordinates (xE, yE, zE).

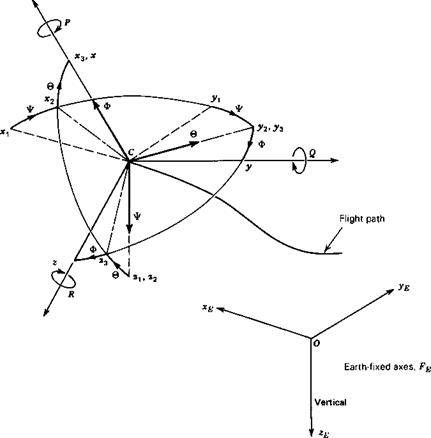
The orientation of the airplane is given by a series of three consecutive rotations, the Euler angles, whose order is important. The airplane is imagined first to be ori­ented so that its axes are parallel to those of FE, (see Fig. 4.2). It is then in the posi­tion Cx^^Zi – The following rotations are then applied.

1. A rotation Ф about oz i, carrying the axes to CX’2y2z2 (bringing Cx to its final azimuth).

2. A rotation ® about oy2, carrying the axes to Cx3y3z3 (bringing Cx to its final elevation).

3. A rotation Ф about ox3, carrying the axes to their final position Cxyz (giving the final angle of bank to the wings).

In order to avoid ambiguities which can otherwise result in the set of angles (ф, в, ф) the ranges are limited to

~ТГ<ф<ТГ or 0^(/r<277

7Г 77

—— < 0< —

2 2

— 77<ф<77 ОГ 0 < <£ < 277

The Euler angles are then unique for most orientations of the vehicle. It should be noted that in a continuous steady rotation, such as rolling, the time variation of ф for example is a discontinuous sawtooth function, and that another exception occurs in a vertical climb or dive, when в = ±77/2. For then (ф, в, ф) = (ф + а, ±77/2, – а) gives the same final orientation regardless of the value of a. The above difficulties can be avoided by using direction cosines3 or quaternions4 to define the orientation of the airplane instead of Euler angles. We use the Euler angles because they give a more physical picture of the airplane attitude than the other alternatives. For a more complete discussion of methods of describing vehicle orientation the reader is re­ferred to Hughes (1986).