Prandtl-Glauert Analysis

8.6.1 Prandtl-Glauert interpretation

The significance of the Ml term in the PG equation (8.60) can be explained as follows. Starting with the velocity V written in terms of the perturbation potential (8.54) we have

IV (V2) • V

Ко (Фхх + фуу + Фхх) = V • V = а = ————————————– 2——- (8.62)

2 а

where the last term is the field source a as given by the compressible continuity equation (8.1). For small – disturbance flows where |V0| ^ 1 we can now make the following approximations to the quantities above.

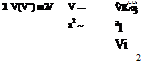V(V2) — 2V2 (фхх x + фху y + фхх z)

Equation (8.62) then simplifies to

фхх + фуу + фХХ — MK фх

which is equivalent to the PG equation (8.60). Hence, the extra Mlфхх term in the PG equation is nothing more than an approximation to the field source distribution a(r). The great simplification here is that this ap­proximate field source is now linearly related (i. e. proportional) to the unknown ф(r) perturbation potential’s derivatives, and as a result can be eliminated through a linear variable transformation as follows.

8.6.2 Prandtl-Glauert transformation

The Prandtl-Glauert transformation applies to the overall flow problem, including the boundary conditions. It has a single scaling parameter

f3 = si I-Ml (8.64)

called the Prandtl-Glauert factor (not to be confused with the sideslip angle). The transformation of the flow problem has the form ф(х, у,х;Мто) ^ ф(х, у,х) where the PG variables denoted by the overbar are defined as follows.

{y| = |вУ| , ф = в2ф (8.65)

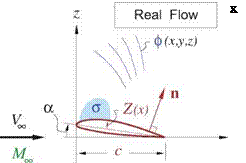
As sketched in Figure 8.12, the geometry is shrunk in y, z by the в factor. This reduces all the geometric angles, aspect ratios, and also the x components of all normal vectors n = {пх пу nz}T by the same factor.

{

пх

пу

Пх

It also gives the following relations between the various derivatives.

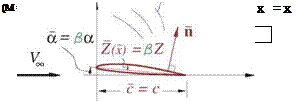Using the above transformation relations converts the PG equation and wall BC in physical space into the Laplace equation and wall BC in the transformed space.

фхх + фуу + фгг	= 0		(8.68)
Wall BC: фуПу + фупг or: фу	= – Пх = Z(х) — cr	(in 2D)	(8.69) (8.70)

Figure 8.12: Prandtl-Glauert transformation from physical variables (left) to PG variables (right).

The fact that a compressible flow looks incompressible after the PG transformation can be explained or interpreted in a number of ways. One explanation is that the perturbation velocity field in the transformed space has zero divergence and zero curl,

а = V ■ (Vф) = 0 (equation (8.68))

uj = V x(Vф) = 0 (identity)

and hence is an incompressible and irrotational flow. Another useful although less rigorous explanation is associated with the thickening effect, which reduces percentage-wise streamtube area variations in the real flow. A low speed flow over a more slender body also has smaller streamtube area variations, so the y, z – scaled incompressible flow mimics the real compressible flow’s more uniform streamtube area distributions.