. Second-Order Approximation

On replacing the spatial derivative of Eq. (1.15) by Eq. (1.22), the finite difference equation to be solved is

Eq. (1.24) is a second-order finite difference equation, the same order as the original partial differential equation. For a unique solution, two boundary conditions are required. This is given by the boundary conditions of the physical problem, Eq. (1.14); i. e.,

u0 = 0, uM = 0. (1.25)

On following Eq. (1.16), a separable solution of a similar form is sought,

U (t) = Re [Uee-lmt]. (1.26)

Substitution of Eq. (1.26) into Eqs. (1.24) and (1.25) leads to the following eigenvalue problem:

U0 = 0, UM = 0.

Two linearly independent solutions of finite difference equation (1.27) in the form of Eq. (1.4) can easily be found. The characteristic equation is

The two roots of Eq. (1.29) are complex conjugates of each other. The absolute value is equal to unity. Thus, the general solution of Eq. (1.27) may be written in the following form:

Ue = A sin (©l) + B cos (©l).

where

Upon imposition of boundary conditions (1.28), it is easy to find

B = 0, A sin (©M) = 0.

For a nontrivial solution, it is required that sin(0M) = 0. Hence,

&M = nn, n = 1, 2, 3,…

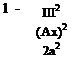or

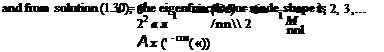This yields

Now, it is instructive to compare finite difference solutions (1.32) and (1.33) with the exact solution of the original partial differential equations (1.20) and (1.21). One obvious difference is that the exact solution has infinitely many eigenfrequencies and eigenfunctions, whereas the finite difference solution supports only a finite number (2M) of such modes. Furthermore, mn of Eq. (1.32) is a good approximation of the exact solution only for nn/M < 1. In other words, a second-order finite difference approximation provides good results only for the low-order long-wave modes. The error increases quickly as n increases.