Special Solutions of the Conservation Equations

Certain special solutions of the basic equations describing an incompressible flow are of great value in applications. We start by looking for an important integral of the equations that provides information regarding the connection between the local pressure and flow speed.

From Chapter 3, the defining equations in Cartesian coordinates for a two­dimensional planar, incompressible, inviscid steady flow are:

continuity: — + — = 0 (3.52)

dx dy

du du dp,

x-momentum: ри—+ pv— = – A – + obx

dx dy dx x

y-momentum: pw-^- + pv dТ = -^T + pby, (3.70)

dx dy dy y

where the density is constant and a body-force term was added to Eq. 3.2 as two components bx and by to make a point (the body-force term is shown to be negligible in most aerodynamics applications and later dropped). The task, then, is to solve this set of three simultaneous partial-differential equations for the three unknowns u, v, and pressure p. In fact, this task is not as difficult as it may first appear.

Consider first the momentum-conservation equations. Rather than write them as two-component equations, as previously, write the vector equation, Eq. 3.66, for a steady, two-dimensional, inviscid flow. Then, Eq. 3.66 becomes:

dV dV „ ,.л,,

pu— + pv— = – Vp-pb. (4.16)

dx dy

The body force is assumed to be the gravity force acting in the downward direction (i. e., the y direction in two dimensions); this is the usual case. Thus, b=g=| g IJ = – gj, where g is the acceleration due to gravity and j is the unit vector in the y-coordinate (upward) direction. Because rectangular coordinates are used, Eq. 4.16 can be written in a more compact vector form as:

p(V-V)V=-Vp-pg. (4.17)

The objective is to directly integrate this form of the momentum equation. Integration can be carried out in a straightforward way under two different assumptions, each of which leads to the same final form of integrated equation. However, the equations actually apply to different sets of physical conditions. Both
assumptions are demonstrated here to emphasize the difference in the applica­bility of the resulting integrated equations. Because the full vector form of the momentum equation is used, the two approaches that follow also are valid in three dimensions.

The first approach is to integrate Eq. 4.17 along a streamline; in this case, the flow may be rotational. The second approach considers integration along any arbi­trary path through the flow field; however, the flow then must be irrotational as demonstrated here.

1. Integration along a streamline:

First expand Eq. 4.17 in standard vector notation, as follows:

P(V»VXm + vj) = – zjp і – – У j + pgj

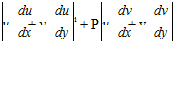
dp. .

ayJ+pgj.

Consider now a general incremental displacement vector ds = dx і + dy j. Taking the vector-dot product of ds with the vector-momentum equation results in:

which is valid along any line in the flow field. Focus on the square bracket on the left side of this equation. Now, require that the length ds is not any arbitrary length but rather is a length ds along a streamline. Recall from the definition of a streamline that a certain relationship between u and v must hold along a stream­line—namely, that:

— = v ^ udy = vdx. dx u

Use this relation in the second and third terms within the square bracket. Substi­tute (udy) for (vdx) in the second term and (vdx) for (udy) in the third term. The result is:

Now, from calculus, if u = u (x, y), then:

, du, du,

du = — dx +—dy. dx dy

The same thing is true for v(x, y) and p(x, y). Thus, the full equation, Eq. 4.18, may be rewritten along a streamline as follows:

p [udu+vdv] = – dp + pgdy udu = d(u2/2), vdv = d(v2/2),

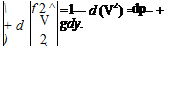so that on dividing through by p, Eq. 4.18 finally becomes:

In Eq. 4.19a, the quantity V is the magnitude of the velocity vector (sometimes referred to as the speed) and the square of V is equal to the sum of the squares of the orthogonal velocity components.

Eq. 4.19a is set aside to derive this same equation in another way. The equation then is integrated. Note that Eq. 4.19a is easy to integrate if the density, p, and the gravitational acceleration are constant.

2. Integration throughout the flow field (irrotational flow only):

The starting point is again Eq. 4.17. Begin by using a standard vector identity that states:

Now, for an irrotational flow, the curl of the velocity vector, VxV = Z, is zero by definition. Hence, for an irrotational flow, the left side of Eq. 4.17 simplifies and the equation becomes:

where again, V is the magnitude of the velocity vector. Taking the vector-dot product of this equation with an arbitrary line segment ds = dxi + dyj yields Eq. 4.17 in the following form:

Again using the basic ideas of calculus, this may be written as follows:

Eqs. 4.19a and 4.19b are identical but arise from different assumptions. Notice that under either assumption, the two partial-differential momentum equations in component form have reduced to a single equation, Eq. 4.19a or 4.19b, which may be integrated easily providing that the density and gravity are constant.

The Bernoulli Equation

Recall that the flows considered here are incompressible. It follows that:

j dp.

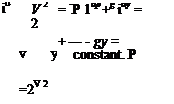Also, assume that the magnitude of the acceleration due to gravity, g, is a constant (to be justified later). Then, integrate Eq. 4.19 as follows:

The integration follows directly because each integral operation simply undoes the differential operation that follows it. Eq. 4.20 is a simple algebraic equation. Consid­ering Eq. 4.19 to be derived along a streamline as in Eq. 4.19a, the most that can be said is that the sum of the three terms in Eq. 4.20 is equal to a constant at any point along a particular streamline. It is not a requirement that this constant is the same among streamlines. However, if irrotationality is assumed as in Eq. 4.19b, then the constant must be the same on every streamline and, hence, throughout the flow field.

Taking two points in the flow field, either along a streamline or in an irrotational flow field, Eq. 4.20 states:

1 T/2 1 T/2

2PV1 +Р1-ВУ1 = 2PV2 + —2 – gy2.

In ordinary aerodynamic problems, the extent of the region of interest around an air­foil or fuselage is not large in the vertical (y) direction, so that (y1 – y2) is small. (This may not be true for a dirigible with large dimensions in the vertical direction!) Thus, in the usual problems of flows around flight vehicles, the gravity-force contribution is negligible and this term, henceforth, is neglected. Eq. 4.20 is written as follows:

1 2

p + 2 pV2 = constant = p o. (4.21)

Eq. 4.21 is the celebrated Bernoulli Equation.[12] It is emphasized that this equation may be used only for an incompressible flow. Serious errors have been made by forgetting this important limitation. It was the incompressible-flow assumption that

allowed the term 1 — to be written as — 1 dp and the integration of the exact dif – PP

ferentials followed directly. If the flow is compressible, other similar but somewhat more complicated equations relating the flow variables may be derived, as accom­plished later. However, for emphasis, the Bernoulli Equation as derived here may not be used to make calculations for a compressible flow.

Now, examine the Bernoulli Equation. If two points are taken in an irrotational flow field, the equation states that the sum of the static-pressure term and the term pV2/2 is equal to the same constant at those two points. If the second point is taken to be a location where the velocity is zero, the pressure term alone appears in the sum at that point. This term is the pressure when the velocity is zero (i. e., when the flow is brought to rest or stagnates), and this pressure is give a special name and
symbol: stagnation pressure = po = pressure where the flow velocity is zero. This ref­erence pressure often is referred to as the total pressure (because it is evaluated by summing two terms) or the “total head” (because pressure is sometimes measured as the height of a liquid column).

Recalling the two different approaches in the derivation of the Bernoulli Equation, it follows that if a flow is rotational (e. g., within a boundary layer), then the stagnation pressure is constant along any streamline within the boundary layer, but the constant is not the same value among streamlines. If a flow is irrotational, the stagnation pressure is the same everywhere in the flow field.

All of the terms in the Bernoulli Equation have the units of pressure because:

slug	" ft2"		lbf s2	" ft2"		‘ lbf"
_ ft3 _	_ s2 _		ft4	_ s2 _		_ ft2 _

Thus, each term in the Bernoulli Equation can be given a descriptive pressure name as follows:

p = static pressure = the pressure in a flow field that would be measured by an instrument moving with the same velocity that the flow is moving at the point in question

рУ2/2 = dynamic pressure = the “pressure” due to fluid motion po = stagnation pressure = the pressure at some point in the flow where the velo­city is zero, as at the stagnation point at the nose of an airfoil or vehicle

These three definitions are fundamental and appear throughout this book. The defi­nitions must be committed to memory and a clear understanding of their physical meaning is vital.

Static pressure at a point must be measured in a way that does not disturb the flow because if the flow is locally slowed or accelerated by the measuring device, then a true measurement cannot be made. One way to measure the static pressure of a flow in a wind-tunnel test section, for example, is to make a small hole (i. e., a static-pressure tap) in the wall of the test section (Fig. 4.6a). The hole should be smooth and small enough to ensure a local measurement, and it is connected by tubing to some suitable pressure-measuring device. Of course, there is a boundary layer growing on the test-section wall, but it is shown in Chapter 8 that the variation of static pressure through this boundary layer in a direction normal to the wall essen­tially is zero. Hence, the static pressure as measured at the wall is that of the external,

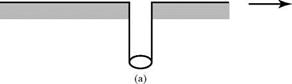static port

(b)
undisturbed flow at a particular streamwise station. If the static pressure is not con­stant across the test section, a local measurement in the flow may be made by using a static-pressure probe (Fig. 4.6b), which is a small tube aligned with the flow and streamlined at the upstream end so as to produce as small a flow disturbance as poss­ible. A static-pressure tap is made in the tube wall several diameters downstream of the front of the probe to allow any local-flow accelerations around the nose to die out. This pressure tap is connected to a suitable pressure-measuring device.

The dynamic pressure cannot be measured directly because it is not a physical quantity but rather is only a variable having the units of pressure. The dynamic pressure can be measured indirectly as the difference between the stagnation pressure and the static pressure.

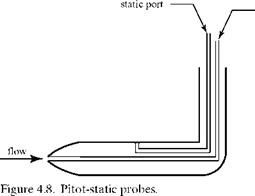
The stagnation pressure in a flow can be measured by using a stagnation-pressure probe (also called a pitot probe or a total head probe), shown in Fig. 4.7. This is simply an open-ended tube aligned with the flow and connected to a pressure-measuring device, which effectively “dead-ends” the tube. The oncoming flow slows and then comes to a rest at the entrance to the tube. The resulting stagnation pressure can be measured by means of an aneroid device or a liquid column.

The simultaneous measurement of stagnation and static pressure allows for the determination of flow velocity through the use of the Bernoulli Equation (providing, or course, that the density is known or can be measured).

This would be a truly local measurement only if the static and stagnation-pres­sure probes were located close to one another. Hence, they are often combined into one instrument, called a pitot-static probe (Fig. 4.8).

The differential (i. e., stagnation minus static) pressure is most often measured by using such a probe because this is more accurate than measuring each pressure independently and then finding the difference between the two values. Again, the static-pressure tap must be located far enough from the nose of the probe that the flow has returned to essentially undisturbed conditions.

The stagnation pressure exists as a physical reality anywhere that the flow is brought to rest (e. g., at the end of a pitot probe or at the stagnation point on an airfoil or wing). However, the stagnation pressure can be defined at any point in the flow field, whether or not the flow there is at rest. Thus, for purposes of calculation, the flow can be thought of as being brought to rest at any convenient point in the flow (whether or not it is physically at rest there) by means of an “imaginary” pitot probe, if this is helpful during the solution of a problem.

It is often convenient to express a physical pressure in terms of a nondimen­sional ratio called the pressure coefficient:

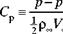
(4.22)

where p is the local static pressure in question and the subscript ^ refers to values of static pressure, density, and velocity in the undisturbed freestream. The density usually is written without a subscript in material pertaining to incompressible flow because for incompressible flow, the density is constant everywhere in the flow field. The dynamic pressure in the denominator of Eq. 4.22 always is formed with the freestream values of velocity and density (which are constants) rather than with local values, which vary throughout a flow. Expressing a pressure in coefficient form conveys considerably more information than just a quoted pressure magni­tude because knowledge of the nondimensional coefficient value allows the predic­tion of the pressure magnitude in a corresponding flow that could have a different freestream velocity and/or freestream static-pressure level.

This definition of the pressure coefficient also is valid for a compressible flow (with the density now carrying an “infinity” subscript), including supersonic flow. Care must be taken in examining plots of chordwise pressure distribution on airfoils
because the convention is to graph the pressure-coefficient ordinate as negative upward. Notice that the pressure coefficient can be either positive or negative, depending on the relative values of the local and freestream static pressures. This is in contrast to the absolute pressure, which never can be negative.

In the case of incompressible, inviscid flow in which the Bernoulli Equation holds and the stagnation pressure is constant everywhere, the pressure coefficient may be written as:

V2

Pressure distributions often are tabulated as the ratio — for incompressible flows.

EXAMPLE 4.9 Given: Air is drawn from the atmosphere at standard sea-level con­ditions (p = 1.225 Kg/m3,p = 1.013 x 105 N/m2) into a wind tunnel by means of a fan at the discharge end (see illustration). It is known that at a certain fan speed, the test-section velocity is 60 m/s. Assume the flow to be steady, incompressible, and inviscid.

Required: Predict (a) the pressure at the stagnation point of a model in the test section, and (b) the static pressure in the test section with the model removed.

Approach: Because the flow is at low speed (and assumed to be incompressible), use the Bernoulli Equation.

Solution: (a) Consider any fluid particle suitably far from the wind-tunnel entrance so that it is initially in the atmosphere at rest and then is sucked into the test section by the inflow. The path of this particle is a streamline along which the stagnation pressure is constant. Far from the entrance, the pressure of the air at rest is atmospheric pressure, so that the stagnation pressure along that streamline is atmospheric pressure. The same is true for any streamline because the flow is assumed to be inviscid and, hence, irrotational. Thus, when the fluid particle is brought to rest at the stagnation point of the model, the pressure there is the stagnation pressure along the stagnation streamline, which in this wind tunnel is equal to the atmospheric pressure. No calculation is necessary.

(b) Consider any streamline and imagine bringing the flow to rest somewhere in the empty test section. The stagnation pressure there is atmospheric pressure, as noted in (a). Apply the Bernoulli Equation at this point:

P + 1pV2 = Po =1.013 x 105 = p +1(1.225)(60)2.

Solving, the static pressure in the empty test section is 9.915 x 104 N/m2.

Appraisal: The static pressure in the test section must be less than the stag­nation (atmospheric) pressure, as indicated by the answer. Careful thought is necessary in this problem to correctly identify static and stagnation pressure (contrast the role of atmospheric pressure in this problem with Example 4.10). In (b), the ability to “imagine” the flow being brought to rest in the test sec­tion—even though there is no stagnation point physically present there— provides the key to the application of the Bernoulli Equation. Now, suppose that air from the atmosphere is pulled into the wind tunnel, but the fan is relo­cated so as to be just downstream of the entrance. Would the answers to the questions be changed? Yes. (The student should give this conclusion careful con­sideration.) In this latter case, work is done on the fluid particles as they pass through the fan, so that the pressure at a stagnation point on the model would not be the same as the atmospheric pressure!

example 4.10 Given: An airplane is in steady flight at 150 mph at an altitude of 15,000 feet (p = 0.0015 slugs/ft3, p = 1,194 lbf/ft2 absolute). The pressure at a certain Point A on the wing is measured at 8.0 psia. Assume a steady, incom­pressible, inviscid flow.

Required: (a) What is the pressure at a stagnation point on the airplane, and (b) what is the velocity at Point A?

Approach: Because the flow is incompressible, use the Bernoulli Equation. Because the flow is assumed to be inviscid, the stagnation pressure is the same everywhere in the flow field.

Solution: The problem is posed from the viewpoint of an observer on the ground watching an airplane fly past. Apply a coordinate transformation such that the airplane is fixed and the air is flowing by. Because the airplane is in steady flight, this transformation is made by imagining that the observer now is riding on the airplane. As the observer looks around at the airplane, it appears to be at rest and there is a wind of 150 mph blowing against the observer’s face (which is the uniform flow from upstream infinity). The atmospheric pressure is unchanged by this shift in observer location. Thus, in this problem with the airplane appar­ently at rest (i. e., body-fixed coordinates), the static pressure of the oncoming flow is the atmospheric pressure and there is a dynamic pressure due to the velo­city of the oncoming flow.

(a) From the Bernoulli Equation:

1 2 1 2

p0 = po„ = p*m+2PV2 = 1,194 + 2(0.0015)[(150)(1.467)]2 = 1,230.3 psfa,

where consistent units require the velocity to be expressed in ft/s.

(b) Again applying the Bernoulli Equation at Point A with po a constant

everywhere:

Po = PoA = Pa+pvA ^ va = 323 ft/s-

Appraisal: The ambient pressure has a completely different role in this example than in the prior one; the two examples should be carefully reviewed until this becomes clear. Steady-flow problems normally are easiest to solve in a “body – axis” system—that is, in which the observer rides with the moving vehicle so that it appears to be at rest.

Return now to the Bernoulli Equation as the integral solution of the momentum equation. The Bernoulli Equation is a simple scalar equation. In particular, if the magnitude of the velocity is known at any point of interest, then the pressure at that point follows directly.

This suggests a strategy for solving the incompressible-flow problem that was posed initially as described by three partial-differential equations. Suppose that the velocity components and, hence, the magnitude of the velocity, at any field point could be found by working with the continuity equation. Then, the substitution of this velocity into the scalar Bernoulli Equation (which represents the integrated effect of the vector-momentum balance) yields the pressure at that point. If needed, the pressure distribution over a body then could be found and integrated to deter­mine important forces, such as the lift on an airfoil.

At first glance, this strategy does not appear to be feasible because two velocity components must be found using only one (continuity) equation. This is where the velocity potential and the stream function become useful. In the next section, the continuity equation is examined with the scalar functions, the velocity potential, and the stream function. It is shown that it is possible to establish a powerful method for evaluating the magnitude of the velocity at any point in the flow field by starting with the continuity equation.