Standing Wave (Modal) Solution

The wave equation governing transverse vibration of a nonuniform string was de­rived in Eq. (2.26) for uniform strings. Here, we repeat it for convenience, with a slight generalization

d2v d2v

Tsx=m(x) Й?

Here, the mass distribution m(x) is allowed to vary along the string. This partial differential equation of motion with two independent variables may be reduced to two ordinary differential equations by making a “separation of variables.” The dependent variable of transverse displacement is represented by

v(x, t) = X(x)Y(t)

This product form is now substituted into the wave equation, Eq. (3.1). To simplify the notation, let ( ) and () denote ordinary derivatives with respect to x and t. Thus, the wave equation becomes

TX"(x)Y(t) = m(x) X(x)Y(t) (3.3)

Rearranging terms as

TX" (x) Y(t)

m(x) X(x) Y(t)

we observe that the left-hand side of this equation is a function of only the single independent variable x and the right-hand side is a function of only t. The presence of m(x) reflects material density and/or geometry that varies along the string, whereas constant T is consistent with approximations used in deriving Eq. (3.1). Because each side of the equation is a function of different independent variables, the only way that the equality can be valid is for each side to be equal to a common constant. Let this constant be – m2, so that

TX"(x) Y(0=_ 2 m(x) X(x) Y(t) —

This yields two ordinary differential equations, given by

TX"(x) + m(x)m2 X(x) = 0 Y(t) + m2 Y(t) = 0

so that the two ordinary differential equations are of the same form; that is

X"(x) + a2 X(x) = 0 Y(t) + m2Y(t) = 0

Because the general solutions to these linear, second-order differential equations are well known, they are written without any further justification as

X(x) = Asin(a x) + B cos(ax) Y(t) = C sin (mt) + D cos (mt)

where

(3.10)

Recall that these solutions are only valid when a = 0.

The boundary conditions on the string are given in Eqs. (2.27). The boundary condition on the left end of the string, where x = 0, can be written as

v(0, t) = X(0)Y(t) = 0 (3.11)

which is satisfied when

X(0) = 0 (3.12)

so that

B = 0 (3.13)

The boundary condition on the right end is

v(t, t) = X(i)Y(t) = 0 (3.14)

which is satisfied when

X(t) = 0 (3.15)

and so

Asin(at) = 0 (3.16)

If A = 0, the displacement is identically zero for all x and t. Although this is an acceptable solution, it is of little interest and therefore is referred to as a “trivial solution.” Of more concern is when

sin(at) = 0 (3.17)

This relationship is called the “characteristic equation” and has a denumerably infinite set of solutions known as “eigenvalues.” These solutions can be written as

a, = у (i = 1, 2,…) (3.18)

where, recalling that a = 0 is a requirement for this solution, we must exclude the root corresponding to i = 0. To ascertain whether a nontrivial a = 0 solution exists, we must return to the first of Eqs. (3.8) and determine whether a nontrivial solution exists with a = 0 that also satisfies all the boundary conditions—that is, whether there is a nontrivial solution to X" = 0 for which X(0) = X(t) = 0. Obviously, there is no such solution for this problem. Solutions associated with a = 0 are addressed in more detail when we consider problems for which rigid-body modes may exist.

Therefore, for each integer value of the index i, there is an eigenvalue ai and an associated solution Xi, called the “eigenfunction.” It contributes to the general solution based on the corresponding value of Yi . Thus, its total contribution can be written as

where
(3.21)
[E sin (ait) + Fi cos (ait)]
where
ai	(3.22)
i n x ~
(3.24)
Фі (x) = sin

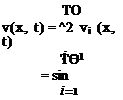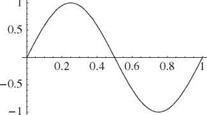
or any constant times фі (x). It can be observed from this function (Fig. 3.1) that the higher the mode number i, the more crossings of the zero axis on the interval 0 < x < І. These crossings are sometimes referred to as “nodes.” The trend of in­creasing numbers of nodes with an increase in the mode number is generally true in structural dynamics.

In the previous solution for the total displacement, each mode shape is multiplied by a function of time. This multiplier is called the “generalized coordinate” and is represented here by ^ (t). For this specific problem, the generalized coordinates are

§i (t) = Ei sin (ait) + Fi cos (ait)

and thus are seen to be simple harmonic functions of time with frequencies ai. Because there were no external loads applied to the string, the preceding result is

Figure 3.1. First three mode shapes for vibrating string

called the “homogeneous solution.” Had there been an external loading, the resulting time dependency of the generalized coordinates would reflect it.

Thus, the total string displacement can be written as a sum of “modal” contri­butions of the form

v(x, t) = Фі (x)Hi (t) (3.26)

І =1

This expression can be interpreted as a weighted sum of the mode shapes, each of which has a modal amplitude (i. e., the generalized coordinate) that is a function of time. For the homogeneous solution obtained here, this time dependency is simple harmonic at a frequency that is unique for each mode or eigenvalue. These are called the “natural frequencies” of the modes, or “modal frequencies,” and are represented by m. For the string, they are

with the lowest frequencies given by the lowest mode numbers. Indeed, just as the increase in the number of nodes with the mode number is generally true, so it is with

the natural frequency. When the physical and geometric parameters of the problem are expressed in any consistent1 set of units, the units of the natural frequency are rad/sec. Division by 2n converts the units of frequency into “cycles per second,” or Hertz. The inverse of the natural frequency in Hertz is the period of the oscillatory motion.

To summarize what has been accomplished in solving the wave equation, it may be said that the string displacement as a function of both x and t can be represented as a sum of modal contributions. Each mode in this representation is a structural dynamic property of the given system (i. e., string) and can be described completely by mode shape and modal frequency. Such “modes of vibration” can be formulated for any linearly elastic structure that is a conservative system. This statement includes two restrictions that must be observed for a modal representation: (1) linearity, which is satisfied here by the linear wave equation; and (2) the system must be conservative, which means that there can be no addition or dissipation of energy in free vibration. A typical violation of the second restriction is the existence of damping, such as structural or aerodynamic damping. When damping is present, it can be adequately treated as an external loading. Mode shapes are determined only by the solution of homogeneous equations and, in general, they are real only for self-adjoint equations.