Symmetric Problem in Subsonic Flow

The fundamental solution is a three dimensional source/sink in subsonic flow. It is related to that in incompressible flow via the Prandtl-Glauert transformation. Hence the perturbation potential at any point in the field is obtained from the surface integral over the wing planform given by (see Ashley and Landhal [7])

where q is the density of source/sink and Lifting Problem in Subsonic Flow

The fundamental solution for this problem is the horseshoe vortex. It consists of two infinitely long vortex filaments of same strength but opposite signs, joined together by an infinitesimal piece of the same strength, Fig. 6.33.

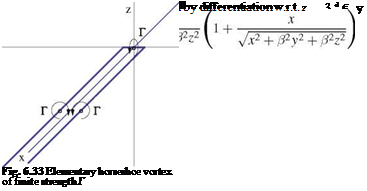The potential for such arrangement can be obtained by integrating a distribution of doublets in the x-direction, with the axis of the doublet in the z-direction

Alternatively, the latter can be obtained directly from Biot-Savart law, as we did before, (see for example Batchelor [8] or Moran [9]).

6.9.1 Extended Lifting Line Theory

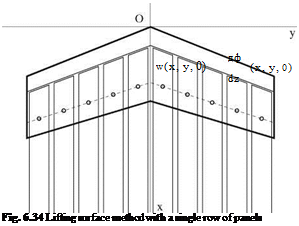
For compressible flows, swept wings are more efficient, since what counts is the velocity component normal to the leading edge. In this case, the lifting line must be modified to take into consideration the sweep angle. A simplified vortex lattice method was used successfully by Weissinger [10] with one row of panels along the loci of the quarter-chord line, as shown in Fig. 6.34. The control points, where the tangency condition is enforced, are located at the three-quarter chord line. Note that, with a single row of panels, one can only represent a flat wing, with zero camber.