THE GENERAL CASE

3.1 INTERCONNECTION OF LFTS • It is first illustrated that the interconnection of various elementary LFTs is also an LFT. Consider the example of Figure 3.2, which rep­resents the way a complete LFT model of the transport aircraft will be obtained in the next chapter. Remember that a complete aircraft model is obtained by adding at the physical outputs the rigid and flexible mod­els (see chapter 2).

An LFT model was separately obtained for both rigid and flexible models. This means that the rigid LFT model contains the physical in­puts й and outputs yr and additional inputs wi and outputs z%, with the fictitious feedback wi = AZ (see Figure 3.2). In the same way, the flexible LFT model contains the physical inputs и and outputs у/ and additional inputs W2 and outputs Z2, with the fictitious feedback W2 = Д2^2- The complete LFT model of the aircraft, у = Fi(H(s),A)u, is computed as an interconnection of the two above LFTs. The augmen­ted model perturbation is Д = diag(Aі, Д2), while H(s) is the transfer matrix between inputs u, w, W2 and outputs y, и i and Z2-

ir*

Figure 3.2. The interconnection of LFTs is an LFT

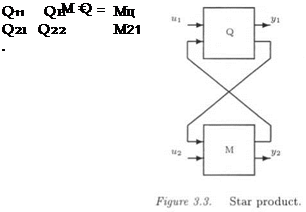
• The star product S(Q, M) of Q and M is defined in Figure 3.3 as a specific interconnection of two LFTs. It corresponds to the transfer
between inputs и і, и 2 and outputs уі, уї-

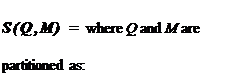Ft(Q, Mn) Qu{I – M11Q22) 1-^12}o1q

m21(i-q22mu)-1Q2i fu(