Vorticity and Curl

The rotation or angular velocity, ю, plays a crucial role in the analysis of flow fields in fluid mechanics. In the analysis equations, the rotation term appears so often together with a factor of 2 that this quantity has been given a special name and notation; thus, vorticity = ^ = 2ю. The factor of 2 enters the definition only for con­venience in relating the vorticity to the curl-vector operation.

In Eq. 4.4, multiply both sides by the factor of 2. The resultant expression is 2ю = |. The right side of the equation is identified from vector analysis as a fun­damental vector operation—namely, the curl of a vector. Thus, vorticity = curl V = V x V. From this, it follows that if a flow is irrotational, then the vorticity is zero and the curl of the velocity vector likewise must be zero.

The expression for vorticity in Cartesian coordinates is:

whereas in plane-polar coordinates, the vorticity vector is given by:

Note that the vorticity vector is normal to the plane of the flow field in a two­dimensional flow.

For a two-dimensional planar field, a flow is irrotational if:

dv du dx dy

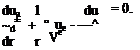whereas in planar-polar coordinates, a flow is irrotational if:

If the differential form of the momentum equation, Eq. 3.66, is written for a two­dimensional incompressible flow with all of the viscous terms detailed on the right side, it may be combined with the continuity equation and the definition of vorticity, Eq. 4.6, and written as a single equation for the time rate of change of vorticity of a moving fluid particle, DZjDt. The resulting equation for DZJDt is called the vorticity – transport equation, which shows that DZjDt is proportional to the coefficient of vis­cosity of the fluid. This means that the vorticity or rotation of a particle moving in a fluid changes because of the presence of viscosity. If attention is focused outside of the boundary layer, where the flow may be represented as inviscid (i. e., a flow with zero viscosity coefficient), the time rate of change of vorticity in this flow is zero. Now, the usual viewpoint for aerodynamics problems is to assume that the vehicle is at rest and that the flow is issuing from upstream infinity as a uniform flow. If the flow from upstream infinity is uniform, then none of the fluid particles coming from infinity has any vorticity because all of the velocity-component derivatives are zero. In an inviscid flow, the vorticity continues to be zero, as discussed previously. We conclude that outside of a thin boundary layer, a subsonic flow may be considered irrotational or to have zero vorticity and rotation.