Axisymmetric Flows and Slender Body Theories

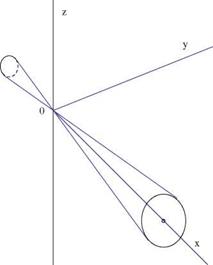
Axisymmetric flows are needed to analyze flow over bodies of revolution. Extensions to bodies of revolution with fins (missiles) or slender wings (low aspect ratio) are also possible, using perturbations of axisymmetric flows. In this chapter, it is natural to use cylindrical coordinates. After the derivation of the governing equations at different Mach number regimes (subsonic, supersonic, transonic), lift and drag are calculated for standard shapes (Fig. 7.1).

7.1 Governing Equations in Cylindrical Coordinates

Assuming steady, inviscid, adiabatic, irrotational and isentropic flow with uniform upstream conditions, the governing equations, in vector notation, are

V.(pV) = 0, VxV = to = 0 (7.1)

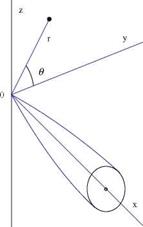
In cylindrical coordinates, Fig. 7.2, the conservation of mass is

(p Ux) + (prur) + (pue) = 0 (7.2)

dx r dr r 89

where (ux, ur, u9 ) are the velocity components in x, r and 9-directions, respectively. The vorticity components are

1 d 1 d

Mx = (rue) – (ur) (7.3)

r dr r d9

1 d d

Mr = (ux) – (u9) (7.4)

r d9 dx

© Springer Science+Business Media Dordrecht 2015

J. J. Chattot and M. M. Hafez, Theoretical and Applied Aerodynamics,

DOI 10.1007/978-94-017-9825-9_7

Notice that Vм = 0, since м = Vx V. The condition is a consequence of the vector identity: the divergence of a curl vanishes.

The density can be calculated from Bernoulli’s law, assuming isentropic conditions

(7.6)

Fig. 7.2 Slender body of revolution and coordinate system

and

Y p V2

+ = H0 = const. (7.7)

Y – 1 P 2

In the latter equation of isoenergetic flow, the potential energy is assumed constant (and does not appear in the total energy).

From the above two equations, one obtains

For the irrotational flow, the velocity can be described by the gradient of a potential function

V = VФ

The potential equation in cylindrical coordinates is given by

The tangency boundary condition on a solid surface is VФ. п = 0, where n is the unit vector normal to the surface. Together with the far field condition, Ф ^ 0, as x2 + r2 ^ to, the formulation is complete.

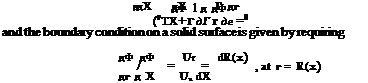For a body of revolution at zero angle of attack, there is no dependency on в, and the governing equation reduces to

or

гдФ _ дФ dR _ 1 дФ dS дг дx dx 2п дx dx

where S(x) = п R2(x), is the cross-sectional area of the body. The pressure coefficient is

and

respectively. Also, the pressure coefficient becomes

(7.21)

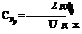
Note that, for body of revolution, д/дв = 0, and the last term in the above equations vanishes.

For incompressible flows (M0 = 0), the fundamental solution of the Laplace equation is

1 1

4n Vx2 + r2

For subsonic flows (M0 < 1), using the Prandtl-Glauert transformation, the fun­damental solution becomes

For a source distribution q(x) per unit length along the x-axis, the perturbation potential at a point (x, r) reads

The strength of the sources is determined through imposing the boundary condition

where S(x) = n R2(x) represents the cross section of the body of revolution. Notice from mass balance, one obtains (see Fig. 7.3)

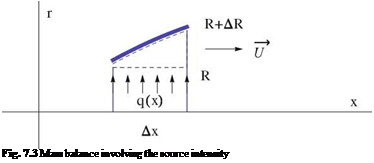q(x)Ax = 2nRAR U = UAS (7.26)

hence

Also, integrating the tangency condition in the proximity of the x-axis (small r)

дф U, U ,

r = S'(x), ^ ф ~ S(x) ln r + g(x) (7.29)

д r 2n 2n

Oswatitsch and Keune [2] provided an approximation of the singular integral leading to

Note that the term g(x) depends in general on M0. For a body with a pointed nose and ending at a point or as a cylinder (S'(l) = 0)

U. (в U fx,, U fl,,

g(x) ~ 2ПS'(x) ln 2 – __ s"(§) ln(x -§)d§ + — S (§) ln(§ – x)d§

0 x (7.31)

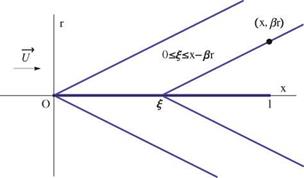
For supersonic flow (M0 > 1), the fundamental solution is different. The solution for a supersonic source is

The potential is a real number only within the Mach cone, Fig. 7.4. A source distribution will give the solution

where the integral is evaluated only for values of § < x – вr, Fig. 7.5.

Von Karman and Moore [3] analyzed this singular integral. Their results are given by

и

Fig. 7.4 Mach cone

Fig. 7.5 Traces of Mach cones in meridian plane

U fx S'(£) – S(x)d£ 2n J0 x – £ £

U, U, в S (x) ln t + S (x) 2n 2n 2x

(7.34)

Ф

Thus, for supersonic flows

U 2n

(7.35)

g(x)