Compressibility Effects
The Mach number M is defined as the ratio of the free-stream velocity to the speed of sound in the undisturbed flow. When an airfoil is operated at M = 1 or higher, the pressure disturbances caused by the airfoil cannot
propagate forward and shock waves form ahead of the airfoil which radically change the pressure distribution around it. Even before an M of 1 is reached, however, weak oblique shock waves can form on the upper surface of the airfoil, for locally at that point the velocity is higher than the free-stream velocity. Just how high depends, of course, on the angle of attack. Hence the M at which the oblique shock waves are first generated also depends on a. The free-stream Mach number at which a local M of 1 is reached on the airfoil is referred to as the critical Mach number, Mcril. Generally, below the critical Mach number, the airfoil section characteristics are not affected appreciably; the possible exception is the slope of the lift curve which increases approximately as l/^/l — M2. Above Mcrit, however, the performance of the airfoil rapidly degenerates. C, max decreases sharply as the drag coefficient increases markedly. Both effects are attributable to
|
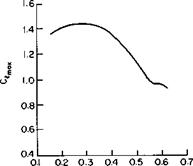
M Fig. 2-25. Effect of Mach number on |
the phenomenon referred to as “shock stall,” which is a separation of the boundary layer on the upper surface resulting from the presence of the oblique shocks.
The severity of the “shock stall” effects is shown in Figs. 2-25 and 2-26, taken from Ref. 8. In Fig. 2-25, for the particular wing tested, it can be seen that C, max decreases from about 1.45 at low M values to 0.68 at an M of
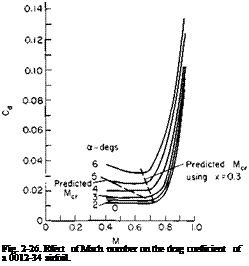
0. 675. From Fig. 2-26 the section Cd for the 0012-34 airfoil is seen to rise rapidly for M values above approximately 0.7, depending on a. In addition, shock stall also shifts the center of pressure, the point of action of the lift force, rearward, thereby causing a significant decrease in the pitching moment.
Generally speaking, we try to avoid exceeding the critical Mach number in rotor and propeller applications for obvious reasons. Hence it becomes important to be able to estimate Mcrit. It is beyond the scope of this book to
delve to any extent into the subject of compressible aerodynamics. For this the reader is referred to the many texts on the subject, such as Ref. 9. Briefly, however, the local velocity, by Bernoulli’s equation, determines the local pressure at each point on the airfoil’s surface. This pressure can be expressed in a dimensionless form as a pressure coefficient Cp.
 |
where p is the local static pressure and p0 is the free-stream static pressure.
At low Mach numbers, again using the incompressible Bernoulli equation, Cp is related to the local velocity v by
The highest v occurs where Cp is a minimum.
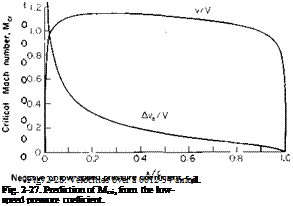
Now, with the isentropic flow relationship of gas dynamics and with some similarity considerations it is possible to relate the minimum value of Cp, Cpmln, obtained at a low Mach number, to the critical Mach number. This relationship is shown in Fig. 2-27. Hence, if we obtain CPm. n, either from subsonic wind-tunnel tests or by potential flow methods, an estimate of Mcrit can be obtained.
Tabulated functions for obtaining airfoil pressure distributions can be found in Refs. 8 and 10, These data are reproduced here for the 0012-34 airfoil in Fig. 2-28. In this figure v/V is the velocity distribution due to
thickness, whereas AvJV is that due to angle of attack. If the section were cambered, still another component, Av/V, would have to be considered, depending on the mean line shape. As tabulated, A vJV is for a C, of 1.0 and for any other C, must be multiplied by C(. Hence Cp is given by
Cp = 1 – (f ± ctI (2’43)
![]()
 |
sign refers to the upper surface.
For an example consider this airfoil at a = 3°. For this angle C, is about 0.3. Using this value of C, and Fig. 2-28, we find with (2-42) that Cpmin occurs at an x of 1.25% and has a value of —0.7. From Fig. 2-27 this value of CPmin results in a predicted critical Mach number of 0.64. In like manner Mcril has been predicted for angles up to 6° and the results superimposed on
Fig. 2-26. At low angles the predicted critical Mach is seen to be slightly less than the “drag divergence” Mach. However, at the higher angles of attack the predicted added effect of a is much greater than the experiment would indicate and is probably attributable to the extremely high values of AvJV predicted near the leading edge. More reasonable agreement is obtained if we calculate Cp at the 30% chord location for each a, which is the location for CPmin for a = 0. These calculations are also shown in Fig. 2-26.
Summary
The material presented in this chapter will find repeated application in the chapters that follow. The continuity, momentum, and energy theorems are all used to analyze the performance of a propeller and of propeller-wing combinations. The characteristics of two – and three-dimensional wings are determined by constructing systems of vortices. The action of the jet flap is explained by combining vortices and sources in a uniform flow to satisfy certain boundary conditions. Even the lift augmentation of the ground – effect machine can be explained by the use of the momentum theory. The analysis of thrust augmentation and cascade systems also depends on the application of the momentum theorem.
Problems
1. A straight-line vortex of strength у extends from the origin to infinity and lies along the x-axis. Find the velocity induced at the point (3, 4, 0).
2. A semiclosed body is formed by placing a source in a uniform flow. What is the relationship between the source strength Q, the uniform velocity V, and the asymptotic width W of the body? Assume two – dimensional flow.
3. By applying the momentum theorem to a circular control surface with a large radius (R -> – зо) enclosing any singular point in the (low (vortices or sources) necessary to construct a closed body with circulation, derive the Kutta-Joukowski law L = pVT and prove D’Alembert’s paradox.
4. A landing-gear strut is circular, with a 2-in. diameter, and 3 ft long. What is its drag at standard sea level (SSL)-conditions at 100 mph? How much drag would be saved by streamlining? How much horsepower does this represent?
5. How thick could a streamline strut be, yet have no more drag than a |-in. circular rod at 100 mph at SSL conditions?
6. An aircraft wing has a 100-ft span and a 16-ft chord. If we assume that the flow, for all intents and purposes, is entirely turbulent over its surface, what would its skin-friction drag be at 200 mph at SSL conditions? What would the drag be if laminar flow could be maintained over the entire surface?
7. Using the pressure coefficient 30% of the chord from the leading edge, predict Mcrit for the 0012-34 airfoil for an angle of attack of 5° and compare with Fig. 2-26.
8. The center of pressure of an airfoil is defined as the point at which the lift is acting to produce the aerodynamic moment on the airfoil. Using Figs. 2-23 and 2-24, determine the Cp location for the 0012 and 66-212 airfoils at a C, of 1.0 (without flaps).
9. Given a fluid motion that rotates like a solid body, that is, the velocity is purely tangential and proportional to the radius
V = cor,
calculate ф and ф. Check your solutions by using them to calculate v.