Elementary Solutions

Recalling the findings of the last section, we proceed to construct a set of elementary solutions to Laplace’s Equation. The corresponding stream-function and velocity potentials are determined, which then form the basis for a powerful problem-solving technique using superposition of the elementary solutions. We start with the simplest and proceed to the more complex flow patterns as we are guided by both physical and geometrical considerations.

Uniform Flow

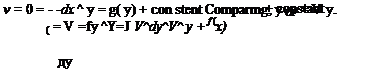For uniform flow, u = VM, v = 0. Thus,

Because f(x) must be zero, the x-axis has been made the zero streamline (i. e., at y = 0, у = 0), so that the constant of integration is zero. The subscript UF designates uni­form flow. Thus, by a similar procedure, ф№ = V^x.

Collecting the results, in Cartesian coordinates,

Iу uf = V~ y (4.29)

1ф№ = Vx.

For many problems, the polar-coordinate form is useful. In this case,

IVUF = V~r sin 0 (4.30)

1фот = V r cos 0.

The student should verify that uniform flow satisfies continuity and is irrotational and that Eqs. 4.29 and 4.30 both satisfy the Laplace’s Equation on substitution.

In what follows, the uniform flow usually is taken as coincident with the x-axis. The results may be extended to uniform flow at an arbitrary angle by letting u = Vx cos a and v = Vx sin a.