Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
. For analysing certain two-dimensional flows, for example the flow over a circular cylinder with and without circulation, it is convenient to work with polar coordinates. The axisymmetric equivalents of polar coordinates are spherical coordinates, for example those used for analysing the flow around spheres. Spherical coordinates are illustrated in Fig. 3.28. In this case none of the coordinate surfaces are plane and the directions of all three velocity components vary over the flow field, depending on the values of the angular coordinates в and ip. In this case the relationships between the velocity components and potential are given by
 |
 |
For axisymmetric flows the variables are independent of в and in this case the continuity equation takes the form
 |
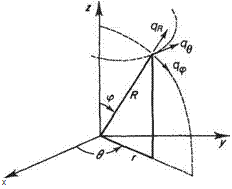Fig. 3.28 Spherical coordinates
 |
 |
 |
Again the relationship between the stream function and the velocity components must be such as to satisfy the continuity Eqn (3.61); hence
