General Wings in Subsonic and Supersonic Flows

To avoid the limitations of thin airfoil theories, the flow must be tangent to the body surface and the singularities should be distributed on the body surface rather than on the axis for a slender body, or on the base surface for a thin wing, for three­dimensional cases. In the panel methods, the body surface is divided into panels and a combination of sources and doublets (with their axis normal to the surface) are used to calculate the flow field, based on approximations of integral equations. In the following, the details for subsonic and supersonic flows are described.

6.11.1 Wings in Subsonic Flows

Panel methods are based on Green’s identities. The derivation starts with Gauss’ theorem (see Ref. [7])

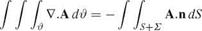(6.140)

where S is the surface of the obstacle and £ is the outer boundary. The volume of fluid in between is denoted by P (the minus sign results from taking the unit normal outward from the solid surface).

Let ф and ф be two continuous functions with continuous first and second deriv­atives in the volume P, and let

J Js+sfydto “ "^l^dS = ///(Ф V 2ф – ф У2Ф) dїї (6.144)

If both ф and ф satisfy the Laplace equation, the right-hand-side vanishes and we have only surface integrals, in terms of ф and ф and their derivatives normal to the surface.

Now, let ф be the potential of a flow over a wing and ф be the potential due to a sink at a point P with coordinates (xP, yP, zP). The potential ф is given by

11

ф = (6.145)

4n rp

where rp = V(x – xp)2 + (y – yp)2 + (z – zp)2.

To apply Green’s identity, the point p must be excluded by centering a sphere a around it with exterior normal, thus

Over the surface a,

(6.147)

and

lim da = 0 (6.148)

a^0 a dn

hence,

In the above formula, the sink term (4^) and the doublet Щ (4^) represent the Green’s functions of the integral equation if the point P is chosen to lie on the surface S, while the integral on S in the far field yields the potential of the uniform flow.

The potential panel methods are based on this integral equation, where = 0 on solid surfaces. After triangulation of the surface, the values of ф at the vertices are calculated from the algebraic equations approximating the integrals, assuming ф is linear over the triangles. other equivalent methods are available in literature.

The above formulation can be extended to subsonic flows via the Prandtl/Glauert transformation.

For lifting problems, special treatment of the vortex sheet is required, where the potential itself is discontinuous. In general, the vortex sheet is floating with the flow and the pressure is continuous across such a sheet. Away from the trailing edge, the sheet will roll up and the vortex core may be modeled in these calculations (the wake can be considered a contact discontinuity and associated jump conditions must be enforced).

Finally, For nonlinear subsonic flows, the governing equation can be rewritten as a Poisson’s equation since

V.(рЧф) = pV2 ф + Vp. V ф = 0 (6.150)

hence

2 1

V 2ф = —V p. V ф = f
p

Iterative methods can be constructed to calculate these flows. The formulation must be extended since V2ф = 0, with an extra term involving volume integrals of the non homogeneous term of the Poisson’s equation. Panel methods become less attractive since three dimensional grids are needed and the convergence of the iterative methods become a problem as the local velocity becomes sonic.

Panel methods for transonic flows are available in literature, where the formulation is based on the unsteady flow equation and artificial viscosity is added in supersonic regions for numerical stability and to capture shock waves. The reader is referred to Refs. [12, 13], for example, for more details.