MORTON’S METHOD

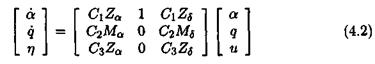This method is illustrated in the specific context of the missile ex­ample. The same result as in the previous subsection is obtained. The idea is to rewrite equations (2.11) of the linearized missile model as:

with:

QS

Mass * V QSd

h

QS

Mass * д

Ma = (1 + ^)М° Ms = (1 + S2)Ms Za = (1+*з)Я“ Zs = (1 + ВД0

As in the previous subsection, the tail deflection input S is renamed as u. Let then:

(4.4)

Equation (4.2) is rewritten as: a q и

(4.5)

with:

Г CxZl 1 CxZg C2Ml 0 C2M$ . C3Z° 0 c3z

(4.6)

Po

and:

Pi P2 Рз

T = uxv{ T = ulv2 T = u2v T – U2v2

Pa

t ui T Щ T Ъ T u2

(4.7)

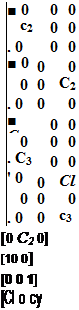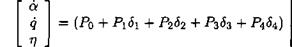
The above equations can thus be rewritten as:

= (Po + BAC) with Д = diag(6i, S2, S3, $4) and:

Let the augmented plant with additional fictitious inputs w and outputs z:

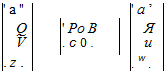
(4.10)

When applying the fictitious feedback w = Az, the initial plant of equation (4.8) is recovered. The LFT model is given in Figure 4.2 (with x = [a, g]).