Prandtl-Glauert equation solution procedure

The great practical importance of the PG transformation is that it allows small-disturbance subsonic com­pressible flow problems which are not transonic (not too close to = 1) to be solved by incompressible potential flow methods. This is accomplished by the following systematic procedure.

1. The real flow problem has geometry defined in x, y, z, with given > 0

2. Scale all y, z dimensions by the PG factor (3 = J 1 — . This gives a transformed geometry in the

PG space X, y, a, with a, nx, AR… all reduced by the same factor of в.

3. Calculate the flow over the transformed geometry using an incompressible flow method and related flow models. These include thin airfoil theory, vortex-lattice, panel, far-field approximations, images, etc. This gives the transformed perturbation potential ф(х, у,г), and/or the transformed perturbation velocities фх, фу, фг, pressures Cp, forces Cl, etc.

4. Calculate the physical perturbation potential and/or velocities using the reverse PG transformations.

(8.71)

д(Ф/02)

dx

д{ф/02)

д(у/Р)

д(Ф/02)

d(z/(3)

With the velocities available, the physical pressure coefficient can now be calculated directly from its exact definition (8.12) . But since the small-disturbance approximation is assumed to be valid here, it’s useful to consider an alternative simplified small-disturbance form based on the asymptotic pressure expression (8.43).

The advantage here is that if the incompressible solution method directly reports the pressures Cp, forces Cl, etc., then the corresponding physical quantities can be obtained immediately. Relations (8.74) and (8.75) are collectively known as Gothert’s Rule [58].

5. To calculate the induced drag coefficient the Trefftz plane wake integral (5.47) can be used, since this only requires that the Trefftz plane’s perturbation flow be incompressible.

|V-V|2/аІ = |Уф|2M£ « 1

This is certainly valid even if itself is not small. Applying the reverse PG transformation to the Trefftz plane wake integral gives the required induced drag transformation rule.

Compressible 2D airfoil

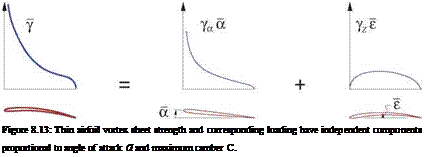
Consider the 2D airfoil problem for compressible flow, shown in Figure 8.12. Assuming the airfoil is very thin for simplicity, its geometry is defined entirely by its Z(x) camberline shape. As discussed in the previous unsteady-flow Chapter 7, and sketched in Figure 8.13, the vortex sheet strength representing the transformed incompressible flow will have the form

5(x) = Ya а + Yz є (8.77)

where ya(x) and Yz(x) are sheet strength distributions for a unit а and a unit camber shape Z(х)/є, respec­tively, with є being the maximum camber value. These unit distributions can be computed a priori. For example, first-order thin airfoil theory as derived in Appendix D gives

7 aO = 2C — — 1

x

and Yz(x) depends in a more complicated manner on the particular unit camber shape. The circulation and lift coefficient will then also have two corresponding independent components.

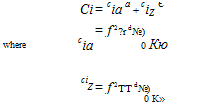(8.78)

(8.79)

(8.80)

The compressible ci is computed by applying the reverse transformations to the solution (8.78).

The final relation (8.82), called Prandtl’s Rule, states that the 2D lift coefficient for the compressible case increases by the factor of 1/в over the incompressible value (ci)inc for that same airfoil. This can be considered a “shortcut method” for 2D cases, since (ci)inc is the incompressible value for the physical (not transformed) airfoil shape and angle of attack. It also applies to calculation of Cp, cm, etc. However, Prandtl’s Rule does not hold for 3D cases, where it is necessary to perform the PG geometry transformation and then use Gothert’s Rule to obtain the correct compressible solution.