Quantification of VRS Effects
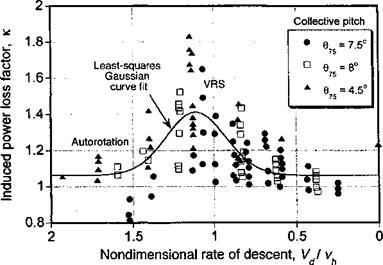
Washizu et al. (1966) have quantified the increased induced power measured during equilibrium descent through the VRS in terms of a power loss factor, к, where
![]() Pi _ CPi T Vi СтХ,-
Pi _ CPi T Vi СтХ,-
where Pi is the induced part of the rotor power and u, refers to the average induced velocity through the rotor as given by the simple momentum theory (see Chapter 2). The induced velocity can be determined from an estimate of the induced power, which is obtained from the measurements of total shaft power by assuming that the profile power, Po, is a function of the rotor thrust alone and does not depend on Vc, that is, in an approach similar to that given in Section 2.13.3 to define the induced power curve in the region where momentum theory is invalid. However, this approach is only approximate and stall effects (which may be produced as a result of the high angles of attack inboard on the blades at high rates of descent) may need to be accounted for. The induced power can then be calculated by subtracting the profile power and loss of potential energy per unit time from the total measured power using C/> = Cp — Cp0 — XcCt, from which the average induced velocity ratio can be obtained from A., = CpJCj – The induced power loss factor then follows from Eq. 5.95 and is essentially a measure of the extra induced power required by the rotor as compared to the momentum theory solution to produce thrust as it descends into its own vortical wake.
The measured values in Fig. 5.30 show the variation of к as a function of descent velocity, where it is noted that a maximum induced loss occurs for this helicopter rotor configuration around a nondimensional descent rate of Vd/vh ^ 1.2 (Vc/vh ^ —1.2). This is consistent with flow visualization and other experimental evidence shown in Section 2.13.6, which suggests that this condition is deeply into the VRS. It is clear also that in autorotation, which is where Vd/vh ^ 1.9, the rotor returns to having a fairly low induced power factor.
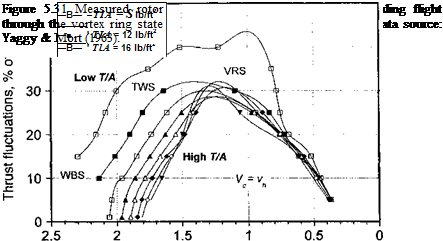
The VRS is accompanied by an extremely unsteady (aperiodic) flow field surrounding the rotor. This behavior is illustrated by the experimental results of Yaggy & Mort (1963), as shown in Fig. 5.31, where the measured rotor thrust fluctuations for a rotor in vertical descent are plotted as a percentage of its mean thrust. At low rates of descent notice that the data essentially collapse to a single curve for all values of disk loading. Because rotor thrust fluctuations in VRS are produced by interactions with its own wake as it comes close to the rotor, then the amplitude of the fluctuations should be related to the mean thrust.
|
Figure 5.30 Measured induced power factor in vertical descending flight through the vortex ring state. Data source: Washizu et al. (1966). |
 |
Nondimensional rate of descent, VJ v.
a h
Therefore, a correlation with disk loading at low rates of descent is to be expected. Notice that the thrust fluctuations build up rapidly as the vertical rate of descent increases, reaching a maximum at Vj/vh ~ 1.2. Thereafter, the fluctuations decrease rapidly as the rotor enters into the turbulent brake state (TWS) and then the windmill brake state (WBS), where the wake is now expanding above the rotor (see also Fig. 14.18).
The experimental results in Fig. 5.31 show a marked dependence on disk loading near VRS, a point discussed by Brown et al. (2002). Disk loading and blade loading (the latter which is related to mean lift coefficients and so to stall proximity) are proportional for a given rotor, and so the observed change in rotor loads with disk loading suggests that the measured data probably contains some evidence of blade stall. This effect is much less clear from the results of Washizu et al. (1966) or Betzina (2001) because there are insufficient data to allow for an interpolation of points to constant values of disk loading. Nearly all of the VRS data in the literature have been obtained from subscale model rotor tests at fixed collective pitch. This makes it difficult to isolate the effects of blade loading on the rotor aerodynamics in the VRS, so to predict how VRS may differ for different rotor configurations (i. e., rotors with different geometric characteristics). However, in nearly all cases the peak amplitude of the unsteady thrust fluctuations lies close to the conditions where the rate of descent is equal to the induced velocity through the rotor.
Yaggy & Mort (1963) also show that a rotor with larger blade twist exhibits larger thrust fluctuations in the VRS. Blade twist affects the distribution of induced velocity over the disk, the position of the tip vortices in the wake and, therefore, the points over the disk that first approach VRS conditions. Leishman et al. (2002) also made this point based on theoretical arguments of wake stability and the onset of wake breakdown in descending
flight. Therefore, it would seem that attempts to generalize the behavior of a rotor as it approaches VRS without reference to the interdependent effects of disk loading or geometric parameters (such as blade planform and blade twist) would be inappropriate.
As previously mentioned, the conditions leading to the onset of the VRS may be obtained under a number of different flight conditions, including situations in forward flight where the rate of descent is low but the disk AoA is high. For example, this situation could be obtained operationally during certain types of maneuvers, such as descending pull – ups at moderate to high airspeeds. Unfortunately, there are fewer experimental results for these conditions: Yet, both the flow visualization of Drees & Hendal (1951) and the thrust nuciuauons measurements оі raggy вс ivion anu oetzina suggest tnat trie
strongest unsteady VRS conditions can be obtained at high rates of descent but with some small forward speed (i. e., a small edgewise component of flow velocity parallel to the disk). The problem, however, is the accurate determination of the induced velocity through the rotor under these conditions.
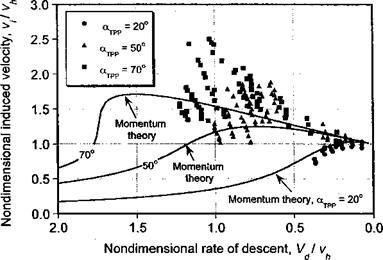
For an inclined descent when the AoA of the disk is otypp, the velocity components normal and parallel to the rotor disk are — VcSinotTpp and Vc cos ajpp, respectively. The results for the induced velocity through the rotor are shown in Fig. 5.32 for a range of AoA. It is interesting that the measurements follow the same trend as given by the momentum theory (Section 2.14.4), although this should not be construed as an endorsement of its applicability in this regime. Momentum theory does, however, underpredict the value of the induced velocity and clearly does not predict the inherent unsteady fluctuations, which is of course a fundamental characteristics of the rotor flow state when in the VRS. Notice that the fluctuations drop off quickly as the disk AoA decreases below 50° and is consistent with piloting experience on helicopters, which shows that a forward speed component causes the rotor to quickly exit the VRS. The results in both Figs. 5.30 and 5.32 are useful in that they provide the analyst with at least some quantifiable basis for estimating the rotor power requirements in steeply descending flight and possibly determining the flight conditions that may result in the phenomenon of “power settling” for a specific type of helicopter.
|
Figure 5.32 Estimated induced velocity in inclined descending flight. Data source: Washizu et al. (1966). |
|
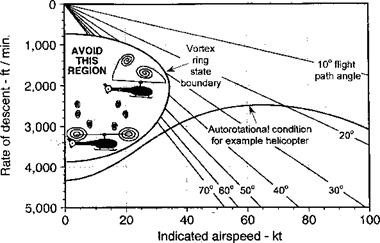
Figure 5.33 The boundary where vortex ring state is encountered is limited to low airspeeds and high rates of descent. Notional data only – does not represent any particular helicopter. |