SOME REMARKS ABOUT THE FLOW OVER THE CYLINDER AND THE SPHERE
The examples of the flow over a cylinder and a sphere clearly demonstrate the principle of superposition as a tool for deriving particular solutions to Laplace’s equation. From the physical point of view, these results fall in a range where potential flow-based calculations are inaccurate owing to flow separation. The pressure distribution around the cylinder, as obtained from Eq. (3.104), is shown in Fig. 3.14 along with some typical experimental results. Clearly, at the frontal stagnation point (0 = л) the results of Eq. (3.104) are close to the experimental data, whereas at the back the difference is large. This is a result of the streamlines not following the surface curvature and separating from this line as shown in Fig. 3.13; this is called flow separation.
The theoretical pressure distribution (Eq. (3.125)) for the sphere, along with the results for the cylinder, are shown in Fig. 3.17. Note that for the three-dimensional case the suction pressures are much smaller (relieving
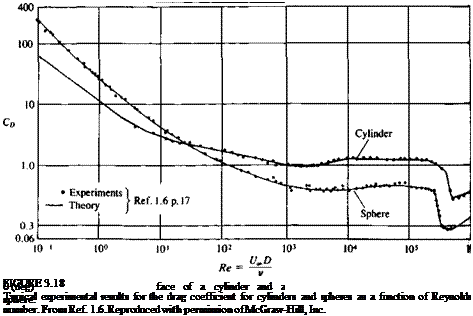 |
effect). Experimental data for the sphere shows that the flow separates too but the low pressure in the rear section is smaller. Consequently, the actual drag coefficient of a sphere is less than that of an equivalent cylinder, as shown in Fig. 3.18 (for Re > 2000). This drag data is a result of the skin friction and flow separation pattern, which is strongly affected by the Reynolds number. Clearly, for the laminar flows (Re < 2000) the drag is large owing to larger flow
separation behind the body, which is being reduced as the turbulent flow momentum transfer increases (Re > 10s, see Schlichting,16 p. 17). Note that the inviscid flow results do not account for flow separation and viscous friction near the body’s surface and therefore the drag coefficient for both cylinder and sphere is zero. This fact disturbed the French mathematician d’Alembert, in the middle of the seventeenth century, who arrived at this conclusion that the drag of a closed body in two-dimensional inviscid incompressible flow is zero (even though he realized that experiments result in a finite drag). Ever since those early days of fluid dynamics this problem has been known as the d’Alembert’s paradox.













