Source Flow

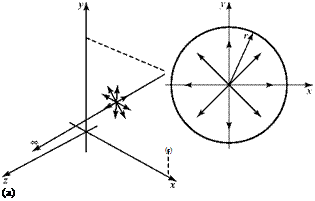
Source flow is flow that is assumed to emanate from a point source. In two­dimensional flow, a line source of infinite length pierces the x-y plane at a point (Fig. 4.9a). This point source in the x-y plane corresponds to outflow from the axis of a cylinder (Fig. 4.9b). In three-dimensional flow, a point source corresponds to out­flow from the center of a sphere (see Chapter 7). Source flow is emitted in a purely radial direction; there is no tangential component of velocity. Thus, the streamlines are all straight lines originating at a point.

Assume two-dimensional planar flow and consider a point source at the origin of coordinates. Let Л be defined as the volume flow rate from the source per unit time per unit depth out of the page. The magnitude of this quantity is the “strength” of the source, which can be adjusted as necessary to match boundary conditions during analysis. If Conservation of Mass is to be satisfied, then for any circle of arbi­trary radius r, about the origin (Fig. 4.9c),

рЛ = mass flux out of source = p(2nr)(1)ur ^ ur =2~>

Figure 4.9. Point source.

where 2n is the circumference of the circle of radius r and the product of this with unity normal to the x-y plane yields the area through which the outflow occurs. By defini­tion, the circumferential velocity u0 = 0. Notice that continuity requires that the radial velocity be proportional to 1/r so that at the source (r = 0), the velocity is infinite. This singularity is not troublesome in constructing flows by super position, as shown later.

Integrating the velocity components yields the following in polar coordinates (i. e., the most convenient coordinates for this flow):

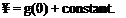n dy

u0= 0 = —-—

0 dr

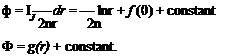Comparing the two expressions for y, it follows that f(r) = 0. The constant of inte­gration may be set to zero for convenience. Similarly,

Comparing, f(0) = 0 and the constant of integration may be set to zero. Summarizing for polar coordinates:

у = — 0
2n

ф =— lnr
2n

and converting to rectangular coordinates:

Л – i

y s = 2Пtan

ф8 = 2Пln ( + /),

where the subscript s designates a source.

Again, substitution shows that Eqs. 4.31 and 4.32 both satisfy the Laplace’s Equation. Considering a circular path enclosing the origin, the circulation around that closed path is zero because there is no component of velocity tangential to the path (u0 = 0). Thus, by Stokes’ Theorem, the source flow is an irrotational flow.

A sink is simply the opposite of a source; that is, the strength Л is negative instead of positive. The radial velocity is inward (negative ur) and the fluid flows into the origin rather than being emitted from the origin. Eqs. 4.31 and 4.32 apply, with a change in sign.

Vortex

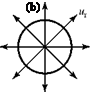
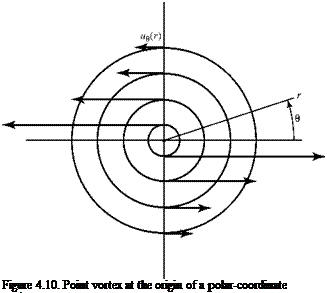
The elementary solution called a vortex was encountered in Example 4.3, where it was shown that a physically possible flow with circular streamlines must have a
tangential velocity that varies inversely as the distance from the center if the flow field is to be irrotational. Figure 4.10 illustrates such a flow field. Thus, ue = K/r and ur = 0. It was not possible to state previously whether the flow is rotational at the exact center. The answer to this question had to await development of the concept of circulation. Because this now is accomplished, we apply the definition of circulation by taking the line integral around a closed path, which is a circle of arbitrary radius r centered at the origin. Then:

2n 2n – jr

Г = – Jv. ds = – J u0 (rd0) = – J K(rdQ)

0 0 r

and, integrating:

Г

Г = -2nK ^ K =——- .

2n

Next, we appeal to Stokes’ Theorem, Eq. 4.10—namely:

r = – J Vds =-JJ (Vx V)-ndS.

C S

Take the surface integral to be over the surface enclosed by the circle and lying in the x-y plane, so that dS in Eq. 4.10 is an element of an area of a circle and the unit vector perpendicular to the surface in the x-y plane is n = k. Furthermore, in the x-y plane, the curl of the velocity vector, V x V, is a vector with a single component per­pendicular to the plane and with a magnitude IV x VI. Then, it follows that:

-Г = 2пК = jj (V x V) • ndS = jj (| V x VI)k • kdS = JJlVx V | dS

s S S

Because within the double integral, the dot product k* k is unity.

Consider now a small circle enclosing the origin. The circulation on the path enclosing this circle is unchanged because for this flow, Г does not depend on r. If the area is small, then the magnitude IV x VI may be assumed to be an average value over the area, and this constant quantity may be taken through the surface integral. Thus, the previous equation becomes:

-Г = 2nK = JjlVx Vi dS = IVxVi jj dS = IV x Vi (nr2).

S S

From this, it follows that:

IVxVI = 2^, r2

which indicates that as r ^ 0, the curl of the velocity vector (i. e., the vorticity) becomes infinite.

The conclusion drawn from this application of Stokes’ Theorem is that a vortex is irrotational everywhere except at the origin, where it is rotational and, in fact, the vorticity is infinite. Note that for any closed curve that does not enclose the origin, the circulation is zero. For any closed curve that does enclose the origin (regardless of shape), the circulation is a constant.

It is demonstrated in Example 4.3 and Eq. 4.33 that for a point vortex:

Then:

where c1 and c2 are arbitrary constants. Comparing, ДЄ) = 0 and the constant of integration may be set equal to zero. A parallel development yields the velocity potential.

Thus, in polar coordinates for a point vortex at the origin:

w,, = — lnr 2n

2te’

whereas in Cartesian coordinates:

Г -1

—- tan 1

2п

where the subscript v denotes a vortex.

The (constant) circulation, Г, around the point vortex is termed the strength of the vortex because the tangential velocity is directly proportional to this arbitrary constant. Again, substitution demonstrates that Eqs. 4.34 and 4.35 are solutions to the Laplace’s Equation.