State-Space Representations

As we said earlier the state-space representation is not unique; we consider four major representations here [2]. These representations would be useful in certain optimization, control design, and parameter-estimation methods.

2.2.2.1.1 Physical Representation

A state-space model of an aircraft has the states as actual response variables like position, velocity, accelerations, Euler angles, flow angles, and so on (Chapter 3, see Appendix A). In such a model the states have physical meaning and they are measurable (or computable from measurable) quantities. State equations result from physical laws governing the process, e. g., aircraft EOM based on Newtonian mechanics, and satellite trajectory dynamics based on Kepler’s laws. These variables are desirable for applications in which feedback is needed, since they are directly measurable; however, the use of actual variables depends on a specific system.

Example 2.7

Let the state-space model of a system be given as

‘ — 1.43	(40 — 1.48)’	x +	—6.3
0.216	—3.7	—12.8

Let C = an identity matrix with a dimension of 2 and D = a null matrix. Study the characteristics of this system by evaluating the eigenvalues.

Solution

The eigenvalues are eig(A) = 2.725, —4.995. This means that one pole of the system is on the right half of the complex s plane, thereby indicating that the system is unstable (Appendix C). If we change the sign of the term (2,1) of the A matrix (i. e., use —0.216) and obtain the eigenvalues, we get eig(A) = —1.135 ± 1.319. Now the system has become stable, because the real part of the complex roots is negative. The system has damped oscillations, because the damping ratio is 0.652 (obtained by using damp(A), and the natural frequency of the dynamic system is 1.74 rad/s). In fact this system describes the short period motion of a light transport aircraft. The elements of matrix A are directly related to the dimensional aerodynamic derivatives (Chapter 4). In fact the term (2,1) is the change in the pitching moment due to a small change in the vertical speed of the aircraft (Chapter 4). For the static stability of the aircraft, this term should be negative. The states are vertical speed (w m/s) and the pitch rate (q rad/s)
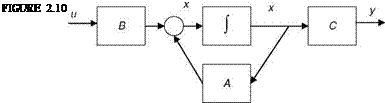
and have obvious physical meaning. In addition, the elements of matrices A and B have physical meaning, as shown in Chapter 5. A block diagram of this state-space representation is given in Figure 2.10.

Writing the detailed equations for this example we obtain

w — — 1.43w + 38.52q — 6.3Se q — Q.216w — 3.7q — 12.8de

We observe from the above equations and Figure 2.10 that the variables w and q inherently provide some feedback to state variables (w, q) and hence signify internally connected control system characteristics of dynamic systems.

2.2.2.1.2 Controllable Canonical Form

In this form, the state variables are the outputs of the integrators (in the classical sense of analog computers, which are now almost obsolete). The inputs to these integrators are differential states (x, etc.). They can be easily obtained from a given TF of the system by inspection:

(2.12)

The corresponding TF is

CmSm + Cm—1Sm 1 + • •• + C1S + CQ

sn + an— 1sn 1 ^•••^ a1s ^ aQ

One can see that the last row of matrix A of Equation 2.1 is the denominator coefficients in the reverse order. This form is so called since this system (model) is controllable, as can be seen from Example 2.8.

Example 2.8

Let the TF of a system be given as

2s2 + 4 s + 7
s3 + 4s2 + 6s + 4

Obtain the controllable canonical state-space form from this TF. Solution

Let y(s)/u(s) = (2s2 + 4s + 7) -3——– 2 ————

‘ s3 + 4s2 + 6s + 4

y(s)/u(s) — (2s2 + 4s + 7)v(s)/u(s) Hence, y(s) — (2s2 + 4s + 7)v(s) and equivalently we have

y(t) — 2€ + 4V + 7v

We define: v — x1, V — x2, and V — x3 and we get

y(t) — 2×3 + 4×2 + 7×1

and x 1 — x2 and x2 — x3. Also, we have v(s) —

V — u(t) — 4V — 6V — 4v
X3 — u(t) — 4×3 — 6×2 — 4×1

Finally, in compact form we have the following state-space form:

y — [7 4 2]x

where x — [x1 x2 x3 xt].

We see that the numerator coefficients of the TF appear in the y-equation, i. e., the observation model and the denominator coefficients appear in the last row of matrix A. It must be recalled here that the denominator of the TF mainly governs the dynamics of the system whereas the numerator mainly shapes the output response. Equivalently, matrix A signifies the dynamics of the system and the vector C the output of the system. We can easily verify that eig(A) and the roots of the denominator of TF have the same numerical values. Since there is no cancellation of any pole with zero of the TF, zeros — roots ([2 4 7]).

space form as Cq — [B AB A2 B…] [2].

For the system to be controllable, the rank of the matrix Cq should be n (the dimension of the state vector), i. e., rank(CQ) — 3. Therefore, this state-space form/system is controllable, hence the name.

2.2.2.1.3 Observable Canonical Form This state-space form is given as

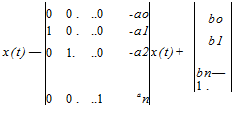
(2.14)

This form is so called because this system (model) is observable as can be seen from the following example:

Example 2.9

Obtain the observable canonical state-space form of the TF of Example 2.8.

Solution

We see that the TF, G(s), is given as (Exercise 2.4)

G(s) — C(sl – A)-1B

Since the TF in this case is a scalar we have [2]

G(s) — [C(sl – A)-1B}T G(s) — BT(si – AT)-1Ct G(s) — Co(sI – AT)-1Bo

Thus, if we use the A, B, C of Solution 2.8 in their ‘‘transpose’’ form we can obtain the observable canonical form:

	0	0	-4		"7"
x —	1	0	-6	x +	4
	0	1	-4		2

u(t); y — [0 0 1]x

The observability matrix of this system is obtained as Ob — obsv(A, C) (in MATLAB)

0	0	1
0	1	4
1	4	10

Since the rank (Ob) — 3, this state-space system is observable, and hence the name for this canonical form.

2.2.2.1.4 Diagonal Canonical Form

It provides decoupled system modes. Matrix A is a diagonal with eigenvalues of the system as the entries.

(2.15)

If the poles are distinct then the diagonal form is possible. We see from this state – space model form that every state is independently controlled by the input and it does not depend on the other states.

Example 2.10

Obtain the canonical variable (diagonal) form of the TF

_ 3s2 + 14s + 14

y(S) — s3 + 7s2 + 14s + 8

Also, obtain the state-space form from the above TF using [A, B,C, D] — f2ss(num, den) and comment on the results.

Solution

The TF can be expanded into its partial fractions [2]:

y(s) — u(s)/(s + 1) + u(s)/(s + 2) + u(s)/(s + 4)

y(t) — [1 1 1]

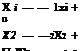Since xi(s) — u(s)/(s + 1), we have

—1	0	0		1
0	—2	0	X +	1
0	0	—4		1

We see from the above diagonal form/representation that each state is independently controlled by input. The eigenvalues are eig(A) as —1, —2, —4 and are the diagonal elements of matrix A. The state-space form from the given TF is directly obtained by [A, B,C, D] — f2ss([3 14 14],[1 7 14 8]) as

We see from the above results that matrix A thus obtained is not the same as the one in the diagonal form. This shows that for the same TF we get different state-space forms, indicating the nonuniqueness of the state-space representation. However, we can quickly verify that the eigenvalues of this new matrix A are identical by using eig(A) — —1,—2,—4. We can also quickly verify that the TFs obtained using the function [num, den] — ss2tf(A, B,C, D,1) for both the state-space representations are the same. The input/output representation is unique as should be the case.