The point doublet and the potential flow around a sphere

A point doublet is produced when the source-sink pair in Fig. 3.30 become infinitely close together. This is closely analogous to line doublet described in Section 3.3.8. Mathematically the expressions for the velocity potential and stream function for a point doublet can be derived from Eqns (3.70) and (3.71) respectively by allowing a —> 0 keeping i — 2Qa fixed. The latter quantity is known as the strength of the doublet.

If a is very small a2 may be neglected compared to 2Ra cos p in Eqn (3.70) then it can be written as

_______________ 1______________

(Л2 cos2 p + R2 sin2 p + 2aRcosp}1^2
1

{Л2 cos2 p + R2 sin2 p — 2aR cos p)

On expanding

Therefore as a —> 0 Eqn (3.72) reduces to

Q

In a similar way write

Rcosp±a (. a

,2 =———— J———

, a a 2 = cos p ± — =F cos V R R

Thus as a —* 0 Eqn (3.71) reduces to

The streamline patterns corresponding to the point doublet are similar to those depicted in Fig. 3.20. It is apparent from this streamline pattern and from the form of Eqn (3.74) that, unlike the point source, the flow field for the doublet is not
omnidirectional. On the contrary the flow field is strongly directional. Moreover, the case analysed above is something of a special case in that the source-sink pair lies on the z axis. In fact the axis of the doublet can be in any direction in three-dimensional space.

For two-dimensional flow it was shown in Section 3.3.9 that the Une doublet placed in a uniform stream produces the potential flow around a circular cylinder. Similarly it will be shown below that a point doublet placed in a uniform stream corresponds to the potential flow around a sphere.

From Eqns (3.65) and (3.73) the velocity potential for a point doublet in a uniform stream, with both the uniform stream and doublet axis aligned in the negative z direction, is given by

дф dR ]_дф R dip

stagnation points be denoted by (Rs, ps). Then from Eqn (3.77) it can be seen that either

The first of these two equations cannot be satisfied as it imphes that Rs is not a positive number. Accordingly, the second of the two equations must hold implying that

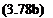ps = 0 and 7Г

It now follows from Eqn (3.76) that

*-(&f

Thus there are two stagnation points on the z axis at equal distances from the origin.

From Eqns (3.66) and (3.74) the stream function for a point doublet in a uniform flow is given by

It follows from substituting Eqns (3.78b) in Eqn (3.79) that at the stagnation points ip = 0.So the streamlines passing through the stagnation points are described by

Equation (3.79) shows that when p ф 0 or тг the radius R of the stream-surface, containing the streamlines that pass through the stagnation points, remains fixed equal to Rs. R can take any value when p = 0 or 7г. Thus these streamlines define the surface of a sphere of radius Rs. This is very similar to the two-dimensional case of the flow over a circular cylinder described in Section 3.3.9.

From Eqns (3.77) and (3.78b) it follows that the velocity on the surface of the sphere is given by

q = 2U sin^

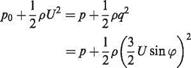So that using the Bernoulli equation gives that

Therefore the pressure variation over the sphere’s surface is given by

(3.81)

Again this result is quite similar to that for the circular cylinder described in Section 3.3.9 and depicted in Fig. 3.23.