Doublet (or Dipole)
 |
|
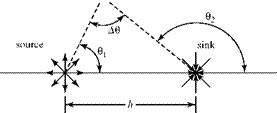
A doublet (or dipole) is defined as a source-sink pair for which the separation distance h ^ 0, whereas the absolute value of the strength, Л, increases such that the
product Q = НЛ remains constant. What this means is that the strength becomes large and the separation distance becomes infinitesimal. Thus, by definition:
Comparing the two expressions for the velocity potential, f(r) = g(0) = constant. Setting the potential function to be zero at 0 = n/2 makes the constant of integration zero, so that:
![]() Q cos 0 2n r
Q cos 0 2n r
![]() Q x
Q x
2n x2 + y2 for polar and rectangular coordinates, respectively. The subscript D denotes a doublet.
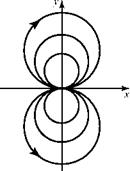
Again, Eqs. 4.37 and 4.38 can be shown to be solutions of Laplace’s Equation by direct substitution. The flow pattern generated by the doublet at the origin, with the source and sink placed on the x-axis, is shown in Fig. 4.13. The flow direction is established by the source being placed on the left side and the sink on the right side.
If the source and sink were located initially on the y-axis instead of the x-axis, the circular streamlines would have been symmetric about the horizontal axis instead of the vertical axis, as depicted in Fig. 4.13, and the axis of the doublet then would be vertical. The doublet shown in the figure is said to have a horizontal axis, meaning that the original source and sink were located on the x-axis.
Four elementary solutions now have been developed and they are collected and tabulated in Table 4.1. It is assumed in this discussion that the source, vortex, and doublet each are located at the origin of coordinates. If it is desired to locate any of them away from the origin, the appropriate expression for the stream function or the velocity potential can be obtained readily from the equations given herein by a simple shifting (i. e., linear transformation) of the appropriate coordinates. It remains to superimpose combinations of these simple Laplace’s Equation solutions to produce solutions for more complicated and interesting flow fields. We also are looking for a way to address the singular points that arise in the elementary solutions. Clearly, these cannot correspond to physically real conditions because, for example, there cannot be point sources with infinite velocity or vortex points with infinite strength.

|
|
Ф |
W |
||||||||
|
Cartesian |
Polar |
Cartesian |
Polar |
u |
v |
Vr |
|||
|
Freestream at a |
V„(x cos a + y sin a) |
V r cos(8 – a) |
V„(y cos a + x sin |
a) |
V r sin(8 – |
a) V cos a |
V sin a |
V cos (8 – a) |
V sin (a – 8) |
|
Source-sink |
ln(*2+^ |
+A 2П ln^) |
±Л tan-‘ f У1 2n ^ x 1 |
T^8 2n |
±Л x |
±Л y |
±Л |
0 |
|
|
2n (x2 + y2) |
2n (x2 + y2) |
2nr |
|||||||
|
Doublet |
К X |
к cos 8 |
к y |
к sin 8 |
к y2 — X2 |
к 2 xy |
к cos 8 |
к sin 8 |
|
|
2n (X2+ y2) |
2n r |
2n (X 2 + y2) |
2n r |
2n (x2 + y2)2 |
2n (x2 + y2)2 |
2n r2 |
2n r2 |
||
|
Vortex |
-f tan-‘ f У1 2n ^ x 1 |
– s8 |
4П ln(*2+y2) |
Г 2n ln^) |
Г y |
Г x |
0 |
Г |
|
|
2n (x2 + y2) |
2n (x2 + y2) |
2nr |














