Geometric Calibration of Camera

4.1.1. Collinearity Equations

After the results of pressure and temperature are extracted from images of PSP and TSP, it is necessary to map the data onto a surface grid in the 3D object space (or physical space) to make the results more useful for design engineers and researchers. The collinearity equations in photogrammetry provide the perspective relationship between the 3D coordinates in the object space and corresponding 2D coordinates in the image plane (Wong 1980; McGlone 1989; Mikhail et al. 2001; Cooper and Robson 2001; Liu 2002). A key problem in quantitative image-based measurements is camera calibration to determine the camera interior and exterior orientation parameters, and lens distortion parameters in the collinearity equations. Simpler resection methods have often been used in PSP and TSP systems to determine the camera exterior orientation parameters under an assumption that the interior orientation and lens distortion parameters are known (Donovan et al. 1993; Le Sant and Merienne 1995). The standard Direct Linear Transformation (DLT) was also used to obtain the interior orientation parameters in addition to the exterior orientation parameters (Bell and McLachlan 1993, 1996). An optimization method for comprehensive camera calibration was developed by Liu et al. (2000), which can determine the exterior orientation, interior orientation and lens distortion parameters (as well as the pixel aspect ratio of a CCD array) from a single image of a 3D target field. The optimization method, combined with the DLT, allows automatic camera calibration without an initial guess of the orientation parameters; this feature particularly facilitates PSP and TSP measurements in wind tunnels. Besides the DLT, a closed-form resection solution given by Zeng and Wang (1992) is also useful for initial estimation of the exterior orientation parameters of a camera based on three known targets.

Figure 5.1 illustrates the perspective relationship between the 3D coordinates (X, Y,Z) in the object space and the corresponding 2D coordinates (x, y) in the image plane. The lens of a camera is modeled by a single point known as the perspective center, the location of which in the object space is (Xc, Yc, Zc). Likewise, the orientation of the camera is characterized by three Euler orientation angles. The orientation angles and location of the perspective center are referred to in photogrammetry as the exterior orientation parameters. On the other hand, the relationship between the perspective center and the image coordinate system is defined by the camera interior orientation parameters, namely, the camera principal distance c and the photogrammetric principal-point location (xp, y ).

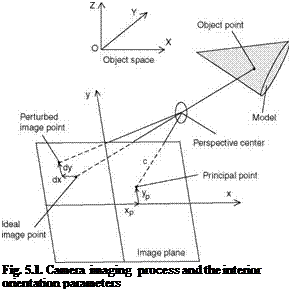The principal distance, which equals the camera focal length for a camera focused at infinity, is the perpendicular distance from the perspective center to the image plane, whereas the photogrammetric principal-point is where a perpendicular line from the perspective center intersects the image plane. Due to lens distortion, however, perturbation to the imaging process leads to departure from collinearity that can be represented by the shifts dx and dy of the image point from its ‘ideal’ position on the image plane. The shifts dx and dy are modeled and characterized by the lens distortion parameters.

The perspective relationship is described by the collinearity equations

(5.1)

where mi} (i, j = 1, 2, 3) are the elements of the rotation matrix that are functions of the Euler orientation angles (т, ф,к),

m11 = cos0 cos к

m12 = sin ю sin ф cos к + cos ю sin к m13 = – cos ю sin ф cos к + sin ю sin к m21 = – ^ф sin к

m22 = – sin ю sin ф sin к + cos ю cos к (5.2)

m23 = cos ю sin ф sin к + sin ю cos к

m31 = sin ф

m32 = – sin ю cos ф

m33 = cos ю cos ф.

The orientation angles (ю, ф,к) are essentially the pitch, yaw, and roll angles of a camera in an established coordinate system. The terms dx and dy are the image coordinate shifts induced by lens distortion, which can be modeled by a sum of the radial distortion and decentering distortion (Fraser 1992; Fryer1989)

dx=dxr + dxd and dy=dyr + dyd, (5.3)

where

dxr = K1(x’-xp )r2 + K2(x’-xp )r4, dyr = K,(y’-yp)r2 + K2( y’-yp)r4 ,

dxd = PJr2 + 2( x – xp )2 ] + 2P2( x – xp )(y’ – yp ), (5.4)

dyd = P2[r2 + 2( y’ – yp )2 ] + 2P,( x – xp )(y’ – yp ), r2 = (x’ – xp )2 + (y’ – yp )2.

Here, K1 and K2 are the radial distortion parameters, P1 and P2 are the decentering distortion parameters, and x’ and y’ are the undistorted coordinates in the image plane. When lens distortion is small, the unknown undistorted coordinates can be approximated by the known distorted coordinates, i. e., x’ « x and y’ ~ y. For large lens distortion, an iterative procedure can be employed to determine the appropriate undistorted coordinates to improve the accuracy of estimation. The following iterative relations can be used: (x’ )0 = x and (y’ )0 = y,

(x’ )k+1 = x + dx[( x’ )k,(y’ )k ] and (y’ )k+1 = y + dy[(x’ )k,(y’ )k ] , where the superscripted iteration index is k = 0,1,2 — .

The collinearity equations Eq. (5.1) contain a set of the camera parameters to be determined by camera calibration; the parameter sets (ю, ф,к, Хc, Yc, Zc), (c, xp, yp ), and (K1,K2,P1,P2) in Eq. (5.1) are the exterior orientation, interior

orientation, and lens distortion parameters of a camera, respectively. Analytical camera calibration techniques have been used to solve the collinearity equations with the lens distortion model for the camera exterior and interior parameters (Ruther 1989; Tsai 1987). Since Eq. (5.1) is non-linear, iterative methods of least – squares estimation have been used as a standard technique for the solution of the collinearity equations in photogrammetry (Wong 1980; McGlone 1989). However, direct recovery of the interior orientation parameters is often impeded by inversion of a nearly singular normal-equation-matrix in least-squares estimation. The singularity of the normal-equation-matrix mainly results from strong correlation between the exterior and interior orientation parameters. In order to reduce the correlation between these parameters and enhance the determinability of (c, x,y ), Fraser (1992) suggested the use of multiple camera

stations, varying image scales, different camera roll angles and a well-distributed target field in three dimensions. These schemes for selecting suitable calibration geometry improve the properties of the normal equation matrix. In general, iterative least-squares methods require a good initial guess to obtain a convergent solution. Mathematically, the singularity problem can be treated using the singular value decomposition that produces the best solution in a least-squares sense. Also, the Levenberg-Marquardt method can stay away to some extent from zero pivots (Marquardt 1963).

Nevertheless, multiple-station, multiple-image methods for camera calibration are not easy to use in a wind tunnel environment where only a limited number of windows are available for cameras and the positions of cameras are fixed. Thus, it is highly desirable for PSP and TSP to have a single-image, easy-to-use calibration method devoid of the singularity problem and an initial guess. In the computer vision community, Tsai’s two-step method is particularly popular. Instead of directly solving the standard collinearity equations Eq. (5.1), Tsai (1987) used a radial alignment constraint to obtain a linear least-squares solution for a subset of the calibration parameters, whereas the rest of the parameters including the radial distortion parameter are estimated by an iterative scheme. Tsai’s method is fast, but less accurate than the standard photogrammetric methods. In addition, the radial alignment constraint prevents this method from incorporating a more general model of lens distortion. Here, we first discuss the DLT that can automatically provide initial values of the camera parameters and then describe an optimization method for more comprehensive calibration of a camera.