Integralgleichung fiir die Zirkulationsverteilung nach der erweiterten Traglinientheorie

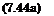
Man kann von der in Кар. 7.22 hergeleiteten Tragflachentheorie zu einer einfacheren Tragflugeltheorie von der Art wie in Кар. 7.1 ge – langen, indem man die iiber die Fliigeltiefe kontinuierlich verteilte Zir – kulation ersetzt durch eine Wirbelhnie, welche an einer geeignet zu wahlenden Stelle der ortlichen Fliigeltiefe angeordnet wird (Trag­linientheorie). Es sei x’i = xt(y’) der Ort dieser tragenden Wirbelhnie, den man zweckmaBigerweise in der Einviertelpunkt-Linie annimmt. Fiir die Funktion G(x, y y’) nach Gl. (7.39a) ergibt sich dann

Dabei ist Г(у’) die gesamte Zirkulation um den Fliigelschnitt yr. Weiter – hin gilt fiir у’ = у und x > x[

0(x, y y) = 2Г(у). (7.44b)

Die kinematische Stromungsbedingung Gl. (7.37) kann in diesem Fall nur noch in einem Punkt langs der Fliigeltiefe erfiillt werden. Die Koordinaten dieses Aufpunktes seien xv(y). Es ist zweckmaBig, diesen Aufpunkt in Dreiviertel der ortlichen Fliigeltiefe anzunehmen (Drei – viertelpunkt, Theorem von Pistolesi), vgl. Кар. 6.351. Damit wird der Klammerausdruck auf der linken Seite von Gl. (7.40)

wobei <x(y) der gegen die Nullauftriebsrichtung gemessene Anstell – winkel ist, Abb. 7.14.

Werden die Gin. (7.45) und (7.44) in Gl. (7.40) eingesetzt, so erhalt man die Integralgleichung fiir die Zirkulationsverteilung nach der

erweiterten Traglinientheorie:

Gegeniiber der in Кар. 7.1 besprochenen einfachen Traglinientheorie hat Gl. (7.46) den groften Vorteil, auch auf schiebende und gepfeilte Fliigel anwendbar zu sein. Diese erweiterte Traglinientheorie wird auch als,,DreiviertelpunJctmethode“ bezeichnet. Sie wurde insbesondere von J. Weissinger [83] ausgearbeitet und angewendet. Mit der Begriindung dieser Traghnientheorie hat sich auch E. Reissner [64] befaBt.

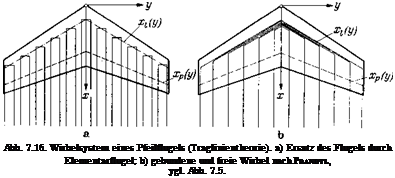Fur den Pfeilfliigel ergibt sich eine Wirbelanordnung nach Abb. 7.16. Dabei ist in Abb. 7.16a der Ersatz des Tragflugels durch das System der Elementarflugel und in Abb. 7.16b das der Prandtlschen Vor – stellung aquivalente Wirbelsystem nach Abb. 7.5 dargestellt.

Bei der Prandtlschen Traglinientheorie und der vorstehend geschilderten Drei – viertelpunktmethode wird der Tragfliigel durch nur eine tragende Linie ersetzt. Von K. Wieghardt [88] stammt der Gedanke, mehrere tragende Wirbellinien hintereinander anzuordnen. Man kann dieses Verfahren als „Mehrpunktmethode“ bezeichnen. N. Scholz [70] hat diese Methode weiter ausgebaut und insbesondere auf den gewolbten Rechteckfliigel angewendet.

Schon friiher hatte V. M. Falkner [9], [10] ein Verfahren angegeben, bei dem sowohl in Tiefen – als auch in Spannweitenrichtung diskrete Wirbel angenommen werden. Weiterhin sei noch auf die Arbeit von W. P. Jones [31] hingewiesen.