Nonlinear Propagation
The noise generated by high performance military aircraft engines is so intense that the propagation of the sound to the far field observer is no longer linear. The earliest evidence of nonlinearity in jet noise was provided by the Olympus engines for the Concorde. Ffowcs Williams et al. (1975) observed a phenomenon they called “crackle.” These were intermittent “intense spasmodic short-duration compressive elements of the wave form.” Though these
|
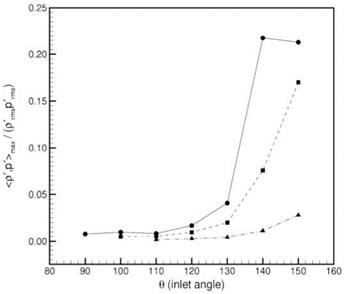
Figure 22. Directivity of normalized (p’,p’)max correlation. Laser probe locations are at r/D = 0, x/D = 12 (Mach 1.8), 10 (Mach 1.4 and Mach 0.95), •, M =1.8; ■, M =1.4; *, M =0.95. (From Tam et al. (2008), with permission). |
are not easily characterized by a change in the spectral shape, the skewness increases and the sound is very annoying. Ffowcs Williams et al. (1975) argued that the source of this change in the signal was associated with wave steepening at the source rather than from nonlinear propagation. However, though the character of the time history is set at the source, nonlinear propagation occurs and does maintain the skewed and annoying nature of the sound into far field.
Methods to predict the nonlinear propagation of jet noise have used the Burgers equation (see Morfey and Howell (1981), Gee (2005), Saxena et al. (2009) and Lee et al. (2010)) and the one-dimensional Navier-Stokes equations (see Wochner et al. (2005)). Morfey and Howell (1981) introduced a nonlinearity parameter that indicates those regions of the spectrum where nonlinear effects are either increasing or decreasing the intensity. However, their solution was based on a knowledge of the spectrum of the noise in the near field rather than the time history, so the propagation results were not
|
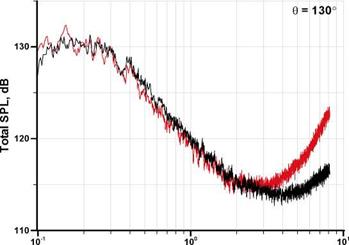
ST Figure 23. Comparison of spectra from sideline microphones at different locations normalized to a fixed distance; M =1.72, and Tt/Ta =2.7. Gray: 25-ft polar, and black: 15-ft constant sideline. (From Viswanathan (2009)). |
satisfactory. The more recent studies make use of the measured time history and then propagate this wave form, using solutions to the Burgers equation, in the same way that sonic boom propagation is calculated. The algorithm used by Gee (2005) is based on the “Anderson algorithm” (see Anderson (1974)). The nonlinear steepening is calculated in the time domain using the “Earnshaw” solution ( Earnshaw (1860)) and the atmospheric absorption effects are calculated in the frequency domain. The calculations by Saxena et al. (2009) and Lee et al. (2010) determine both the nonlinear and atmospheric absorption effects in the frequency domain. This has computational and accuracy advantages as shown by Lee et al. (2010). The effects of nonlinear propagation are best seen when the experimental data are represented in lossless or standard day form and propagated linearly to a common observer location. A good example is shown in Figure 23 from Viswanathan et al. (2009). Here, measurements in a jet with M =1.72 and Tt/Ta =2.7 are shown for a microphone distances of 15 and 25 feet. If linear propagation were present at all frequencies then the curves would fall on top of each other (assuming that the measurements are in the far field). However, it is clear that at high frequencies the curves don’t collapse. This is evidence on the presence of nonlinear propagation. Care should be taken not to assume that the spectra shown are “as-measured” spectra. The lift at high frequencies is purely because the data have been made lossless assuming linear propagation. The “as-measured” spectra would still show a roll-off at high frequencies, but it would be less rapid if nonlinear propagation were present.
6 Acknowledgements
These notes are based on a earlier version written by the authors that was intended to be part of a book on high speed jets. We have added some new material and some topics have been removed to prevent excessive length. For example; jet noise reduction, dual-stream jets, and non-circular jets are not discussed. The authors plan to add these topics to a future publication that emphasizes progress in jet noise modeling, prediction and experiments in the last ten years. The original version was reviewed by Prof. Geoffrey M. Lilley who, as always, offered some valuable and insightful criticism.