Steady Flow

Once the Kutta condition is satisfied, the picture of the flow field remains the same, which means the flow is steady. In a steady flow around airfoil as stated before, there is a bound vortex and the starting vortex. Since the starting vortex is located far away from the profile it has practically no effect. The only vortex in effect is the vortex sheets of upper and lower surfaces. If the thickness of the profile is <12%, it is assumed that the upper and lower surface vortex sheets are close enough and they add up to a single vortex sheet which is easily modeled as a vortex sheet of strength ya. That means, for yu showing the upper surface vortex sheet strength and c showing the lower surface then they add up to

Ca(x) = Cu(x) + Cl(x)-

With this mathematical modeling the Kutta condition and the Laplace’s equations, Eq. 2.15, are both satisfied. Figure 3.5 shows the vortex sheet modeling an airfoil with its chord is in line with x axis and has length of 2b.

According to the Biot-Savart law (Kuethe and Chow 1998), the vortex sheet of strength ya(x) and length di induces the differential velocity of dV at a point (x, z).

Ca (x

2nr

The x and z components of dV reads as

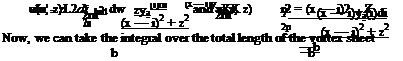du’ = dV sine, dw = —dV cos в, sinh = z/r and cosh = (x — <f)/r. The induced components, from Fig. 3.5, can be expresses as

At this stage, it is essential to note that there is no contribution to the pertur­bation velocities from the free stream speed. If we closely examine the sign of z in the integrands of the above integrals we see that u is antisymmetric and w is symmetric. That is

u (x, 0+) = — u'(x, 0 ) and w(x, 0+) = w(x, 0 )

Let us now find the relation between the perturbation speed u and the vortex sheet strength as follows

The rectangle shown with the dimensions of dx. dz has the circulation given as

ya(x)dx = [U + u'(x, 0+)]dx — (w + dw)dz — [U + u'(x, 0—)]dx + wdz = [u'(x, 0+)— u'(x, 0—)]dx — dwdz

Neglecting the second order terms we get

ya(x) = u'(x, 0+) — u'(x, 0—) = 2u'(x, 0+) (3-1)

Equation 3.1 tells us that the perturbation speed in x direction is given by the local vortex sheet strength. In addition, the physical meaning of a vortex sheet strength is that it is the discontinuity of the velocity between the upper and lower surfaces.

Let us now find the downwash at the surface, z = 0,

b

1 Уд(ПЖ

2p x — П

—b

The integral given in Eq. 3.2 has an integrable singularity at x = П. These type of singular integrals are called the Cauchy type integrals and in Appendix 3 we show how to evaluate this type of integrals at the complex plane.

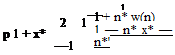Equation 3.2 is an integral equation if we consider ya(x) as unknown function and w(x) as the known downwash. This type of integral equation is called Fred­holm type and its inversion is provided in Appendix 2. Accordingly, if we use the non dimensional coordinates x* = x/b and П* = П/b and utilize the Eq. 3a, b of Appendix 3 we obtain the inverted form of 3.2 as

Equation 3.3 satisfies the Kutta condition at the trailing edge because it has a zero value as x* takes the value of 1. The integrand in the equation is obtained from Eq. 2.20. In case of steady flows the downwash is function of angle of attack, free stream speed U and camber of the airfoil.

After finding an expression for the bound vortex sheet we can now relate it with the lifting pressure coefficient. For the steady flow the pressure coefficient was given by Eq. 2.21 as

cp(x)

Let us now find the lifting pressure cPa as the pressure difference between the lower and upper pressures

The lifting pressure coefficient can be expressed in terms of the upper and lower perturbation speeds. With the aid of Eq. 3.1

According to Eq. 3.5, the lifting pressure coefficient behaves similar to that of the vortex sheet strength. This behavior can be seen with a limiting process applied at the leading and the trailing edges as follows

lim [cpa(x)] = lim — and lim[cpa(x)] = lim — = 0

x!-b £—0 e x – Ь £!0

With these limiting values we see that the singular lifting pressure at the leading edge becomes zero at the trailing edge. Now, the sectional lifting force i can be found using Eq. 3.5 with integration

b b b

1 = 2P“u2 / cpa (x)dx = Pi U j Ca(x)dx where Ca(x)dx (3.6)

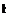
b

gives: І = р? иГа which is known as the Kutta-Joukowski theorem which gives the lifting force acting on a vortex immersed in a free stream speed U and has a strength Г (Kuethe and Chow 1998). If we combine Eqs. 3.3 and 3.6 we obtain the bound vortex sheet strength given in terms of the downwash distribution as follows.

1

Га = -2b J -1

Example 1 For an airfoil at an angle of attack a find (i) sectional lift coefficient, (ii) moment coefficient and (iii) center of pressure and aerodynamic center.

Solution: This the flat plate immersed in a free stream of U with angle of attack a as shown in the following figure.

Equation 3.8 for x0 = 0 gives

Cmo pa

(iii) The center of pressure xCP in terms of this moment reads as

m0

xcp — x0 i

in general. Using the result of (ii) for the flat plate

b

xcp

This result proves that for a symmetric thin airfoil the center of pressure is located at the quarter chord point. Now, let us find the aerodynamic center xac.

By definition the aerodynamic center is the point where the sectional moment is independent of the angle of attack a. With Eq. 3.8 and 9mo/9a = 0 gives us xac = —b/2. This again proves that the aerodynamic center and the center of pressure are at the same points for a symmetric thin airfoil.

Hitherto, we have given the formulation for the steady flow for which flow conditions remain the same with respect to time. When the flow conditions change slowly with time, we can assume quasi steady flow as it happens for a slow change in the angle of attack so the force and the moment change in phase with the angle of attack. The picture is not the same when the changes are fast because we observe a lag between the motion and the response of the airfoil to the motion. Let us now extend our external flow model for the unsteady treatments which gives us the lag as well as the deviations from the steady flow conditions because the presence of near wake effects.