Summary of Chapter 7

First, the governing equations are derived in cylindrical coordinates. The full potential equation and the small disturbance theory are followed including calculations of wave drag and optimum shapes (due to von Karman and Sears and Haaks) for bodies of revolution in supersonic flows. Slender wings of low aspect ratios, including swept and oblique wings, wing-body combinations and slender bodies with general cross­sections are also discussed.

The transonic area rule, involving lift, as well as the supersonic area rule are briefly covered.

Finally, conical flows are studied using the full potential equation and small dis­turbance approximation, as well as numerical solution of the conical Euler equations.

7.9 Problems

7.11.1

According to slender body theory, the fuselage does not contribute to lift, but con­tributes to the pitching moment.

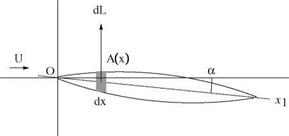
Show that the fuselage moment is given by (see Fig. 7.28)

M, of = pU 2 & f a

where, & f is the volume of the fuselage.

z Fig. 7.28 Moment of a body of revolution at incidence

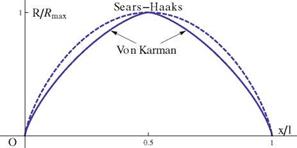
Fig. 7.29 Geometries of two pointed bodies

7.11.2

Consider two bodies pointed at both ends, the Sears-Haaks body and a body obtained by combining two Von Karman ogives (VK-KV), one facing forward and the other facing backward, see Fig. 7.29. The equation for the latter can be described as

S'(x) = 2l A^J(1 – 2х), 0 < x < 2
S'(x) = —2l A. J (2х – 1)(2 – 2х), 2 < x < i

corresponding to two elliptic distributions. Calculate the wave drag of the VK-KV configuration and compare to the Sears-Haaks body for the same maximum cross section. Hint: one approach is to calculate the Fourier coefficients in terms of A with a computer algebra system such as Mathematica to find the drag as

П12 “

ArefCow = – nA2„

n=1

In particular show that

1

A1 = 0, A2 = A, A3 = 0, A4 = — —, …