Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
SWEPT WINGS
For highly swept wings it is necessary to use Weissinger’s method to determine the aerodynamic loading. For approximate solutions, however, the modified Schrenk’s method4-53 given by Pope and Haney offers great simplification and fair accuracy. In many occasions, the strip theory is sufficiently accurate.
Besides the change in lift curve slope as shown by Eqs. 6, 7, 8 and 16 of § 4.3, swept wings differ aeroelastically from normal wings in the effective angle of attack due to elastic deformation (Eq. 5, § 4.4):
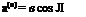
3w. ,
sin Л
Bs
where 9wjds is the slope of the deflection curve in the spanwise direction. Hence, whenever Л Ф 0 (Fig. 4.8), the effective angle of attack, and hence the aerodynamic loading, depends on the bending deflection as well as on the torsional deflection. The effect of the bending deflection can be seen qualitatively as follows. For a sweptback wing (Л > 0), an increase in angle of attack a(r) yields a positive slope 9wjds and hence reduces a(e). This, together with the reduction of the lift curve slope due to Л, means that the wing is not so easily twisted as a normal wing. Thus the sweep – back increases the torsional stability. Hence, the divergence speed is increased by sweepback. For a sweptforward wing (Л < 0), the effect of bending tends to decrease the divergence speed, whereas the reduction of lift curve slope tends to increase it. Generally, the divergence speed is decreased by sweepforward.
On the other hand, for a positive (downward) aileron deflection, dwjds is again positive and a(e) is again reduced if Л > 0, and increased if Л < 0. Accordingly, the effect of bending has a tendency to make the aileron less or more effective according to Л > 0 or Л < 0, respectively. In other words, the effect of bending tends to have the aileron efficiency and the aileron reversal speed reduced by sweepback and increased by sweepforward. Whether a wing’s reversal speed would actually be reduced by sweepback or not depends on the balance between several opposing influences, and a careful analysis is required.
For a cantilever wing with the wing root fixed in space, dw/ds vanishes at the wing root because of the clamping boundary conditions. It increases to a maximum toward the wing tip. Hence, the aforesaid effect of sweep is more seriously felt near the wing tip. It is therefore obvious that, when the pitching angle a(r) of the airplane is increased, the effect of sweepback is to unload the wing tips, and to cause the center of pressure of the wing to move forward. For a sweptforward wing, the load near the wing tip is increased by the elastic bending, and the center of pressure moves forward towards the wing tips. This shift of wing center of pressure has very important effect on the airplane stability.
Detailed presentation of the effects of sweepback and sweepforward can be found in Refs. 4.6, 4.10, 4.26-35.
